题目内容
 已知四棱锥P-ABCD的底面是平行四边形,AD=2AB,∠ABC=60°,PA⊥面ABCD,且PA=AD.若E为PC中点,F为线段PD上的点,且PF=2FD.
已知四棱锥P-ABCD的底面是平行四边形,AD=2AB,∠ABC=60°,PA⊥面ABCD,且PA=AD.若E为PC中点,F为线段PD上的点,且PF=2FD.(1)求证:BE∥平面ACF;
(2)求PC与平面PAD所成角的正弦值.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间角
分析:(1)连结BD交AC于O,取PF中点G,连结OF,BG,EG,利用EO,EG分别为BG,FC的中位线,得到它们对应平行,进而得到平面BEG与平面ACF平行,再由面面平行的性质得到线面平行.
(2)要求线面角,需要先找到线面角的代表角,即过C点做面PAD的垂线,因为PA垂直于底面,所以过C作线段AD的垂线与AD交于H,则CH垂直于面PAD,所以角CPH即为线面角的代表角,要求该角的正弦值,就需要求出PC与CH,可以利用△PAC和△ACH为直角三角形通过勾股定理求出,进而得到线面角的正弦值.
(2)要求线面角,需要先找到线面角的代表角,即过C点做面PAD的垂线,因为PA垂直于底面,所以过C作线段AD的垂线与AD交于H,则CH垂直于面PAD,所以角CPH即为线面角的代表角,要求该角的正弦值,就需要求出PC与CH,可以利用△PAC和△ACH为直角三角形通过勾股定理求出,进而得到线面角的正弦值.
解答:
(1)证明:连结BD交AC于点O,
取PF的中点G,连结OF,BG,EG,
∵O,F分别是DB,DG的中点,∴OF∥BG,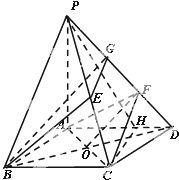
∵E,G分别是PC,PF的中点,∴EG∥CF,
∴平面BEG∥平面ACF,
又∵BE?平面BEG,
∴BE∥平面ACF.
(2)∵BC=2AB,∠ABC=60°,
∴∠BAC=90°.
过C作AD的垂线,垂足为H,则CH⊥AD,CH⊥PA,
∴CH⊥平面PAD.
∴∠CPH为PC与平面PAD所成的角.
设AB=1,则BC=2,AC=
,PC=
,CH=
,
∴sin∠CPH=
=
,即为所求.
取PF的中点G,连结OF,BG,EG,
∵O,F分别是DB,DG的中点,∴OF∥BG,

∵E,G分别是PC,PF的中点,∴EG∥CF,
∴平面BEG∥平面ACF,
又∵BE?平面BEG,
∴BE∥平面ACF.
(2)∵BC=2AB,∠ABC=60°,
∴∠BAC=90°.
过C作AD的垂线,垂足为H,则CH⊥AD,CH⊥PA,
∴CH⊥平面PAD.
∴∠CPH为PC与平面PAD所成的角.
设AB=1,则BC=2,AC=
| 3 |
| 7 |
| ||
| 2 |
∴sin∠CPH=
| CH |
| PC |
| ||
| 14 |
点评:本题考查直线与平面平行的证明,考查直线与平面所成角的正弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
设变量x,y满足约束条件
,则z=2x+y的最大值为( )
|
| A、-3 | ||
B、
| ||
| C、6 | ||
| D、10 |
下列有关命题的说法正确的是( )
| A、命题“若x2>1,则x>1”的否命题为“若x2>1,则x≤1” |
| B、“x=-1”是“x2-2x+3=0”的必要不充分条件 |
| C、命题“?x∈R,使得x2+x+1<0”的否定是“?x∈R,均有x2+x+1<0” |
| D、命题“若x=y,则cosx=cosy”的逆否命题为真命题 |
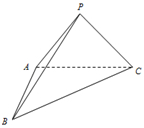 如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC=3,AB=2
如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC=3,AB=2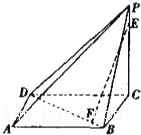 已知四棱锥P-ABCD中,PC⊥底面ABCD,PC=2,且底面ABCD是边长为1的正方形.E是最短的侧棱PC上的动点.
已知四棱锥P-ABCD中,PC⊥底面ABCD,PC=2,且底面ABCD是边长为1的正方形.E是最短的侧棱PC上的动点.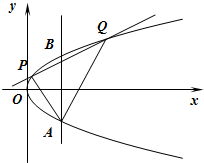 如图,两条相交线段AB、PQ的四个端点都在抛物线y2=x上,其中,直线AB的方程为x=m,直线PQ的方程为y=
如图,两条相交线段AB、PQ的四个端点都在抛物线y2=x上,其中,直线AB的方程为x=m,直线PQ的方程为y=
 给定椭圆C:
给定椭圆C: