题目内容
已知函数f(x)=
sinxcosx+cos2x+
.
(1)求f(x)的最小正周期,并求出当x∈[
,
]时,函数f(x)的值域;
(2)当x∈[
,
]时,若f(x)=
,求f(x-
)的值.
| 3 |
| 1 |
| 2 |
(1)求f(x)的最小正周期,并求出当x∈[
| π |
| 6 |
| π |
| 2 |
(2)当x∈[
| π |
| 6 |
| π |
| 2 |
| 8 |
| 5 |
| π |
| 12 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)化简函数f (x)=
sinxcosx+cos2x+
.为一个角的一个三角函数的形式,然后求f (x)的周期以及函数的值域;
(2)利用f(x)=
,求出sin(2x+
)的值,以及余弦函数值,然后利用两角和与差的三角函数求解f(x-
)的值.
| 3 |
| 1 |
| 2 |
(2)利用f(x)=
| 8 |
| 5 |
| π |
| 6 |
| π |
| 12 |
解答:
解:(1)函数f(x)=
sinxcosx+cos2x+
=
sin2x+
+
=sin(2x+
)+1,
∴T=
=π,
由
≤x≤
得
≤2x+
≤
,
∴sin(2x+
)∈[-
,1].
当x∈[
,
]时,函数f(x)的值域[
,2];
(2)f(x)=sin(2x+
)+1=
,则sin(2x+
)=
;
x∈[
,
],
≤2x+
≤
,
∴cos(2x+
)=-
=-
…(9分)
f(x-
)=sin2x+1…(10分)
=sin(2x+
-
)+1
=sin(2x+
)cos
-cos(2x+
)sin
+1…(11分)
=
+
…(13分)
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∴T=
| 2π |
| 2 |
由
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| 7π |
| 6 |
∴sin(2x+
| π |
| 6 |
| 1 |
| 2 |
当x∈[
| π |
| 6 |
| π |
| 2 |
| 1 |
| 2 |
(2)f(x)=sin(2x+
| π |
| 6 |
| 8 |
| 5 |
| π |
| 6 |
| 3 |
| 5 |
x∈[
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| 7π |
| 6 |
∴cos(2x+
| π |
| 6 |
1-(
|
| 4 |
| 5 |
f(x-
| π |
| 12 |
=sin(2x+
| π |
| 6 |
| π |
| 6 |
=sin(2x+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
=
3
| ||
| 10 |
| 7 |
| 5 |
点评:本题考查两角和与差的三角函数,三角函数的周期以及函数的值域,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
不等式x(x-3)<0的解集是( )
| A、{x|x<0} |
| B、{x|x<3} |
| C、{x|0<x<3} |
| D、{x|x<0或x>3} |
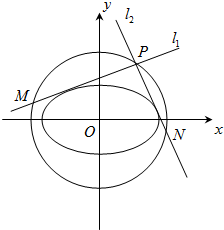 给定椭圆C:
给定椭圆C: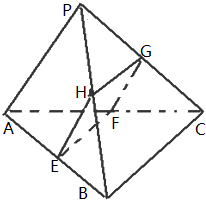 如图,已知点P是三角形ABC所在平面外一点,且PA=BC=1,截面EFGH分别平行于PA,BC(点E,F,G,H分在棱AB,AC,PC,PB上)
如图,已知点P是三角形ABC所在平面外一点,且PA=BC=1,截面EFGH分别平行于PA,BC(点E,F,G,H分在棱AB,AC,PC,PB上)