题目内容
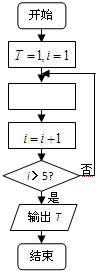 如图所示的程序框图,若执行的运算是1×
如图所示的程序框图,若执行的运算是1×| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| A、T=T•i | ||
| B、T=T•(i+1) | ||
C、T=T•
| ||
D、T=T•
|
考点:程序框图
专题:算法和程序框图
分析:算法的功能是求1×
×
×
×
的值,根据终止程序运行的i=6,可确定执行框应填内容.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
解答:
解:根据算法的功能是求1×
×
×
×
的值,又终止程序运行的i=6,
∴执行框应填内容为T=T•
.
故选:D.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
∴执行框应填内容为T=T•
| 1 |
| i |
故选:D.
点评:本题考查了循环结构的程序框图,根据框图的流程与算法的功能来判断执行框的内容是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列有关命题的说法正确的是( )
| A、命题“若x2>1,则x>1”的否命题为“若x2>1,则x≤1” |
| B、“x=-1”是“x2-2x+3=0”的必要不充分条件 |
| C、命题“?x∈R,使得x2+x+1<0”的否定是“?x∈R,均有x2+x+1<0” |
| D、命题“若x=y,则cosx=cosy”的逆否命题为真命题 |
若函数f(x)(x∈R)是奇函数,函数g(x)(x∈R)是偶函数,则一定成立的是( )
| A、函数f[g(x)]是奇函数 |
| B、函数g[f(x)]是奇函数 |
| C、函数f[f(x)]是奇函数 |
| D、函数g[g(x)]是奇函数 |
y=f(x)是定义在R上的函数,若a∈R,则“x≠a”是“f(x)≠f(a)”成立的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
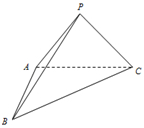 如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC=3,AB=2
如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC=3,AB=2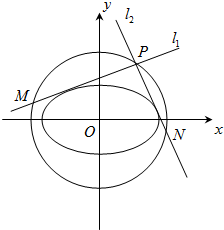 给定椭圆C:
给定椭圆C: