题目内容
13.已知圆x2+y2=r2,直线l:y=x+$\sqrt{2}$,当圆上恰有三个点到直线l的距离都为1时,则r=2.分析 先求出圆心(0,0)到直线l的距离d=1,由圆上恰有三个点到直线l的距离都为1,得到圆心(0,0)到直线l的距离d=$\frac{r}{2}$,由此能出r的值.
解答 解:∵圆x2+y2=r2,直线l:y=x+$\sqrt{2}$,
∴圆心(0,0)到直线l的距离d=$\frac{|\sqrt{2}|}{\sqrt{2}}$=1,
∵圆上恰有三个点到直线l的距离都为1,
∴圆心(0,0)到直线l的距离d=$\frac{r}{2}$,
即$\frac{r}{2}$=1,解得r=2.
故答案为:2.
点评 本题考查圆的半径的求法,是基础题,解题时要认真审题,注意圆的性质、点到直线距离公式的合理运用.

练习册系列答案
相关题目
3.在复平面内,复数$\frac{2-i}{1-i}$(i是虚数单位)对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,PA=AB,E,F,H分别是棱PA,PB,AD的中点,且过E,F,H的平面截四棱锥P-ABCD所得截面面积为$\frac{{3\sqrt{2}}}{2}$,则四棱锥P-ABCD的体积为( )
| A. | $\frac{8}{3}$ | B. | 8 | C. | $8\sqrt{3}$ | D. | $24\sqrt{3}$ |
1.已知曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的渐近线方程为y=±$\frac{\sqrt{2}}{2}$x,则该曲线的离心率为( )
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\sqrt{3}$ |
18.若(1+2x)(1-2x)7=a0+a1x+a2x2+…+a8x8,则a0+a1+a2+…+a7的值为( )
| A. | -2 | B. | -3 | C. | 253 | D. | 126 |
2.定义在R上的函数y=f(x)在(-∞,a)上是增函数,函数y=f(x+a)是偶函数,当x1<x2且x1+x2>2a时,有( )
| A. | f(2a-x1)<f(2a-x2) | B. | f(2a-x1)>f(2a-x2) | C. | f(2a-x1)=f(2a-x2) | D. | 以上都不正确 |
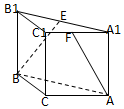 如图,ABC-A1B1C1是直三棱柱,∠BCA=90°,点E、F分别是A1B1、A1C1的中点,若BC=CA=AA1,则BE与AF所成角的余弦值为$\frac{\sqrt{30}}{10}$.
如图,ABC-A1B1C1是直三棱柱,∠BCA=90°,点E、F分别是A1B1、A1C1的中点,若BC=CA=AA1,则BE与AF所成角的余弦值为$\frac{\sqrt{30}}{10}$.