题目内容
20.已知f(x)是定义在R上的奇函数,f(x)满足f(x+2)=-f(x),当0≤x≤1时,f(x)=x,则f(37.5)等于-0.5.分析 根据题意,由f(x+2)=-f(x)可得f(x+4)=-f(x+2)=f(x),即函数f(x)的周期为4,即有f(37.5)=f(1.5),结合题意可得f(1.5)=f[2+(-0.5)]=-f(-0.5),结合函数的奇偶性可得f(0.5)=-f(-0.5),进而结合函数在0≤x≤1上的解析式可得f(0.5)的值,综合即可得答案.
解答 解:根据题意,由于f(x+2)=-f(x),则有f(x+4)=-f(x+2)=f(x),即函数f(x)的周期为4,
则有f(37.5)=f(1.5+4×9)=f(1.5),
又由f(x+2)=-f(x),则有f(1.5)=f[2+(-0.5)]=-f(-0.5),
又由函数为奇函数,则f(0.5)=-f(-0.5),
又由当0≤x≤1时,f(x)=x,则f(0.5)=0.5;
则有f(37.5)=f(1.5)=-f(-0.5)=f(0.5)=0.5,
故f(37.5)=0.5;
故答案为:0.5.
点评 本题考查函数奇偶性的应用,涉及函数的周期性的应用,关键是求出函数f(x)的周期.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
10.设等差数列{an}的前n项和为Sn,若2a3=3+a1,则S9的值为( )
| A. | 15 | B. | 27 | C. | 30 | D. | 40 |
11.下列选项中说法正确的是( )
| A. | 命题“p∨q为真”是命题“p∧q为真”的必要条件 | |
| B. | 向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}•\overrightarrow{b}>0$,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为锐角 | |
| C. | 若am2≤bm2,则a≤b | |
| D. | “?x0∈R,x02-x0≤0”的否定是“?x∈R,x2-x≥0” |
15.在区间[0,1]上随机选取两个数x和y,则y>2x的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
12.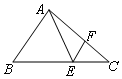 如图,在△ABC中,E,F分别是边BC,AC上的点,且△ABE是边长为3的正三角形,EF∥AB,EF=1,则sinC等于( )
如图,在△ABC中,E,F分别是边BC,AC上的点,且△ABE是边长为3的正三角形,EF∥AB,EF=1,则sinC等于( )
 如图,在△ABC中,E,F分别是边BC,AC上的点,且△ABE是边长为3的正三角形,EF∥AB,EF=1,则sinC等于( )
如图,在△ABC中,E,F分别是边BC,AC上的点,且△ABE是边长为3的正三角形,EF∥AB,EF=1,则sinC等于( )| A. | $\frac{{\sqrt{7}}}{14}$ | B. | $\frac{{\sqrt{7}}}{7}$ | C. | $\frac{{\sqrt{21}}}{14}$ | D. | $\frac{{\sqrt{21}}}{7}$ |
10.已知函数$f(x)=\frac{1}{3}m{x^3}+\frac{1}{2}n{x^2}+x+2017$,其中m∈{2,4,6,8},n∈{1,3,5,7},从这些函数中任取不同的两个函数,在它们在(1,f(1))处的切线相互平行的概率是( )
| A. | $\frac{7}{120}$ | B. | $\frac{7}{60}$ | C. | $\frac{7}{30}$ | D. | 以上都不对 |