题目内容
14.已知函数f(x)=x+1+|3-x|,x≥-1.(I)求不等式f(x)≤6的解集;
(Ⅱ)若f(x)的最小值为n,正数a,b满足2nab=a+2b,求2a+b的最小值.
分析 (Ⅰ)根据题意,由绝对值的性质可以将f(x)≤6转化可得$\left\{\begin{array}{l}{x-1+(3-x)≤6}\\{-1≤x<3}\end{array}\right.$或$\left\{\begin{array}{l}{x+1+(x-3)≤6}\\{x≥3}\end{array}\right.$,解可得x的范围,即可得答案;
(Ⅱ)根据题意,由函数f(x)的解析式分析可得f(x)的最小值为4,即n=4;进而可得正数a,b满足8ab=a+2b,即$\frac{1}{b}$+$\frac{2}{a}$=8,将2a+b变形可得2a+b=$\frac{1}{8}$($\frac{2a}{b}$+$\frac{2b}{a}$+5),由基本不等式的性质可得2a+b的最小值,即可得答案.
解答 解:(Ⅰ)根据题意,函数f(x)=x+1+|3-x|,x≥-1.
若f(x)≤6,则有$\left\{\begin{array}{l}{x-1+(3-x)≤6}\\{-1≤x<3}\end{array}\right.$或$\left\{\begin{array}{l}{x+1+(x-3)≤6}\\{x≥3}\end{array}\right.$,
解可得-1≤x≤4,
故原不等式的解集为{x|-1≤x≤4};
(Ⅱ)函数f(x)=x+1+|3-x|=$\left\{\begin{array}{l}{4,-1≤x<3}\\{2x-2,x≥3}\end{array}\right.$,
分析可得f(x)的最小值为4,即n=4;
则正数a,b满足8ab=a+2b,即$\frac{1}{b}$+$\frac{2}{a}$=8,
2a+b=$\frac{1}{8}$($\frac{1}{b}$+$\frac{2}{a}$)(2a+b)=$\frac{1}{8}$($\frac{2a}{b}$+$\frac{2b}{a}$+5)≥$\frac{1}{8}$(5+2$\sqrt{\frac{2a}{b}•\frac{2b}{a}}$)=$\frac{9}{8}$;
即2a+b的最小值为$\frac{9}{8}$.
点评 本题考查绝对值不等式的解法,涉及基本不等式的性质与应用,关键是正确求出函数f(x)的最小值.

| A. | $\frac{8}{3}$ | B. | 8 | C. | $8\sqrt{3}$ | D. | $24\sqrt{3}$ |
| A. | f(2a-x1)<f(2a-x2) | B. | f(2a-x1)>f(2a-x2) | C. | f(2a-x1)=f(2a-x2) | D. | 以上都不正确 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
表1:甲方案
| 考核内容 | M(文化) | N(面试) | ||
| 得分 | 100 | 80 | 50 | 20 |
| 概率 | $\frac{3}{4}$ | $\frac{1}{4}$ | $\frac{3}{4}$ | $\frac{1}{4}$ |
| 考核内容 | M(文化) | N(面试) | ||
| 得分 | 90 | 60 | 30 | 10 |
| 概率 | $\frac{9}{10}$ | $\frac{1}{10}$ | $\frac{9}{10}$ | $\frac{1}{10}$ |
(I)若该同学希望获得保送资格,应该选择哪个方案?请说明理由,并求其在该方案下 获得保送资格的概率;
(II)若该同学选用乙方案,求其所得成绩X的分布列及其数学期望EX.
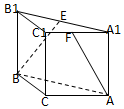 如图,ABC-A1B1C1是直三棱柱,∠BCA=90°,点E、F分别是A1B1、A1C1的中点,若BC=CA=AA1,则BE与AF所成角的余弦值为$\frac{\sqrt{30}}{10}$.
如图,ABC-A1B1C1是直三棱柱,∠BCA=90°,点E、F分别是A1B1、A1C1的中点,若BC=CA=AA1,则BE与AF所成角的余弦值为$\frac{\sqrt{30}}{10}$.