题目内容
如图,动物园要围成相同面积的长方形虎笼四间.一面可利用原有的墙,其他各面用钢筋网围成.
(1) 现有可围成36m长的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼的面积最大?
(2) 若使每间虎笼的面积为24m2,则每间虎笼的长、宽各设计为多少时,可使围成的四间虎笼的钢筋网总长最小?

解:(1) 设每间虎笼长为xm,宽为ym,
则 面积S=xy.
面积S=xy.
由于2x+3y≥2 =2
=2 ,所以2
,所以2 ≤18,得xy≤
≤18,得xy≤ ,即S≤
,即S≤ ,当且仅当2x=3y时取等号.
,当且仅当2x=3y时取等号.
则
所以每间虎笼长、宽分别为4.5m、3m时,可使面积最大.
(2) 设围成四间虎笼的钢筋网总长为lm,则l=4x+6y,且xy=24,所以l=4x+6y=2(2x+3y)≥2×2 =4
=4 =4×
=4× =48(m),当且仅当2x=3y时取等号.
=48(m),当且仅当2x=3y时取等号.
 故每间虎笼长、宽分别为6m、4m时,可使钢筋网的总长最小为48m.
故每间虎笼长、宽分别为6m、4m时,可使钢筋网的总长最小为48m.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
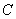 的焦点是
的焦点是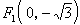 ,
,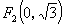 ,点
,点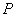 在椭圆上且满足
在椭圆上且满足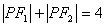 .
.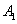 、
、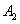 ,右顶点为
,右顶点为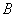 ,圆
,圆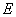 与以线段
与以线段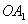 为直径的圆关于直线
为直径的圆关于直线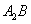 对称.求圆
对称.求圆 ,试求解下列问题.
,试求解下列问题.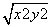 的最大值和最小值;
的最大值和最小值; 的最大值和最小值;
的最大值和最小值; 则
则 的取值范围是________.
的取值范围是________. (x>2)的图象过点A(3,7),则此函数的最小值是________.
(x>2)的图象过点A(3,7),则此函数的最小值是________. 的展开式奇数项的二项式系数之和为128,求展开式中二项式系数最大项.
的展开式奇数项的二项式系数之和为128,求展开式中二项式系数最大项.