题目内容
16.已知a,b∈R,且ex+1≥ax+b对?x∈R恒成立(其中e为自然对数的底数),则ab的最大值为( )| A. | $\frac{1}{2}{e^3}$ | B. | $\frac{{\sqrt{2}}}{2}{e^3}$ | C. | $\frac{{\sqrt{3}}}{2}{e^3}$ | D. | e3 |
分析 当a=0时,此时ab=0; 当a>0时,由题结合(1)得ab≤2a2-a2lna,设(a)=2a2-a2lna(a>0),问题转化为求g(a)的最大值,利用导函数即可
解答 解:设f(x)=ex+1-ax
当a=0时,此时ab=0;
当a>0时,ex+1≥ax+b对?x∈R恒成立,得b≤fmin(x),
∵fmin(x)=f(-1+lna)=2a-alna,
∴b≤2a-alna,
∴ab≤2a2-a2lna,
设g(a)=2a2-a2lna(a>0),
∴g′(a)=4a-(2alna+a)=3a-2alna,
由于a>0,令g′(a)=0,得lna=$\frac{3}{2}$,从而a=${e}^{\frac{3}{2}}$,
当a∈(0,${e}^{\frac{3}{2}}$)时,g′(a)>0,g(a)单调递增;
当a∈(${e}^{\frac{3}{2}}$,+∞)时,g′(a)<0,g(a)单调递减.
∴gmax(a)=$\frac{{e}^{3}}{2}$,即a=${e}^{\frac{3}{2}}$,b=$\frac{1}{2}$${e}^{\frac{3}{2}}$时,ab的最大值为$\frac{{e}^{3}}{2}$.
故选:A.
点评 本题考查函数的单调性及最值,利用导函数来研究函数的单调性是解题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
6.已知过曲线$\left\{\begin{array}{l}{x=3sinθ}\\{y=3cosθ}\end{array}\right.$(θ为参数,0≤θ≤π)上一点P与原点O的直线PO的倾斜角为$\frac{π}{2}$,则P点坐标是( )
| A. | (0,3) | B. | $(-\frac{12}{5},-\frac{12}{5})$ | C. | (-3,0) | D. | $(\frac{12}{5},\frac{12}{5})$ |
11.设集合A={-1,0,1,2,3},B={x|x2-2x>0},则A∩(∁RB)=( )
| A. | {-1,3} | B. | {0,1,2} | C. | {1,2,3} | D. | {0,1,2,3} |
8.复数$\frac{{(1-i{)^2}}}{3-i}$的值是( )
| A. | $-\frac{1}{4}+\frac{3}{4}i$ | B. | $\frac{1}{4}-\frac{3}{4}i$ | C. | $-\frac{1}{5}+\frac{3}{5}i$ | D. | $\frac{1}{5}-\frac{3}{5}i$ |
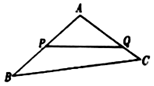 如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.