题目内容
7.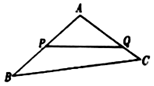 如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.(1)若围墙AP、AQ总长度为200米,如何可使得三角形地块APQ面积最大?
(2)已知竹篱笆长为$50\sqrt{3}$米,AP段围墙高1米,AQ段围墙高2米,造价均为每平方米100元,求围墙总造价的取值范围.
分析 (1)设AP=x(米),则AQ=200-x,得${S_{△APQ}}=\frac{1}{2}x({200-x})sin{120^0}≤\frac{{\sqrt{3}}}{4}{({\frac{200}{2}})^2}=2500\sqrt{3}$(米2)即可
(2)由正弦定理$\frac{AP}{sin∠AQP}=\frac{AQ}{sin∠APQ}=\frac{PQ}{sin∠A}$,得AP=100sin∠AQP,AQ=100sin∠APQ故围墙总造价$y=100({AP+2AQ})=10000({sin∠AQP+2sin∠APQ})=10000\sqrt{3}cos∠AQP$,由$0<∠AQP<\frac{π}{3}$,$\frac{{\sqrt{3}}}{2}<\sqrt{3}cos∠AQP<\sqrt{3}$,得y∈$({5000\sqrt{3},10000\sqrt{3}})$.
解答 解:(1)设AP=x(米),则AQ=200-x,
所以${S_{△APQ}}=\frac{1}{2}x({200-x})sin{120^0}≤\frac{{\sqrt{3}}}{4}{({\frac{200}{2}})^2}=2500\sqrt{3}$(米2)
当且仅当x=200-x时,取等号.
即AP=AQ=100(米),${S_{max}}=2500\sqrt{3}$(米2).…(6分)
(2)由正弦定理$\frac{AP}{sin∠AQP}=\frac{AQ}{sin∠APQ}=\frac{PQ}{sin∠A}$,得AP=100sin∠AQP,AQ=100sin∠APQ
故围墙总造价$y=100({AP+2AQ})=10000({sin∠AQP+2sin∠APQ})=10000\sqrt{3}cos∠AQP$
因为AP≥AQ,所以$0<∠AQP<\frac{π}{3}$,∴$\frac{{\sqrt{3}}}{2}<\sqrt{3}cos∠AQP<\sqrt{3}$,
所以y∈$({5000\sqrt{3},10000\sqrt{3}})$.
答:围墙总造价的取值范围为$({5000\sqrt{3},10000\sqrt{3}})$(元).…(14分)
点评 本题考查了解三角形在实际问题中的应用,基本不等式的应用,考查了转化思想,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 3 | B. | $\frac{\sqrt{13}+1}{2}$ | C. | 6 | D. | 2$\sqrt{2}$ |
| A. | 最小值为$-\frac{1}{2}$,其图象关于点$({\frac{π}{4},0})$对称 | |
| B. | 最大值为$\frac{{\sqrt{2}}}{2}$,其图象关于直线$x=-\frac{π}{8}$对称 | |
| C. | 最小正周期为2π,其图象关于点$({\frac{3π}{4},0})$对称 | |
| D. | 最小正周期为π,其图象关于直线$x=-\frac{3π}{8}$对称 |
 已知全集U=R,集合A={x|x(x+2)<0},B={x||x|≤1},则如图阴影部分表示的集合是( )
已知全集U=R,集合A={x|x(x+2)<0},B={x||x|≤1},则如图阴影部分表示的集合是( )| A. | (-2,1) | B. | [-1,0]∪[1,2) | C. | (-2,-1)∪[0,1] | D. | [0,1] |
| A. | $\frac{1}{2}{e^3}$ | B. | $\frac{{\sqrt{2}}}{2}{e^3}$ | C. | $\frac{{\sqrt{3}}}{2}{e^3}$ | D. | e3 |
| A. | $\frac{4}{3}$ | B. | $\frac{{4\sqrt{3}}}{3}$ | C. | 4 | D. | $\frac{{4\sqrt{6}}}{3}$ |
 在△ABC中,∠B=$\frac{π}{6}$,AC=$\sqrt{5}$,D是AB边上一点,CD=2,△ACD的面积为2,∠ACD为锐角,则BC=$\frac{8\sqrt{5}}{5}$.
在△ABC中,∠B=$\frac{π}{6}$,AC=$\sqrt{5}$,D是AB边上一点,CD=2,△ACD的面积为2,∠ACD为锐角,则BC=$\frac{8\sqrt{5}}{5}$.