题目内容
5.已知向量$\overrightarrow{a}$=(sin(ωx+φ),2),$\overrightarrow{b}$=(1,cos(ωx+φ)),(ω>0,0<φ<$\frac{π}{4}$),函数f(x)=($\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-$\overrightarrow{b}$)的图象过点M(1,$\frac{7}{2}$),且相邻两对称轴之间的距离为2.(Ⅰ)求f(x)的表达式;
(Ⅱ)求f(x)在[-$\frac{2}{3}$,2]上的最大值,并求出此时x的值.
分析 (Ⅰ)根据平面向量数量积公式并化简三角函数式,得到解析式;
(Ⅱ)利用(Ⅰ)的解析式得到角度范围,利用正弦函数的有界性求最大值.
解答 解:(Ⅰ)因为f(x)=($\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-$\overrightarrow{b}$)=${\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}$=sin2(ωx+φ)-cos2(ωx+φ)+3
=3-cos(2ωx+2φ),由相邻两对称轴之间的距离为2.得到周期为4,所以ω=$\frac{π}{4}$,又过(1,$\frac{7}{2}$),
得到sin2φ=$\frac{1}{2}$,因为0<φ<$\frac{π}{4}$,所以2φ=$\frac{π}{6}$;
所以f(x)=3-cos($\frac{π}{2}x+\frac{π}{6}$);
(Ⅱ)因为x∈[-$\frac{2}{3}$,2],所以$\frac{π}{2}x+\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{7}{6}π$],
所以当$\frac{π}{2}x+\frac{π}{6}=π$时即x=$\frac{5}{3}$时函数取得最大值为3-(-1)=4.
点评 本题考查了平面向量的数量积的坐标运算以及三角函数的解析式化简、三角函数的性质;属于中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
16.已知a,b∈R,且ex+1≥ax+b对?x∈R恒成立(其中e为自然对数的底数),则ab的最大值为( )
| A. | $\frac{1}{2}{e^3}$ | B. | $\frac{{\sqrt{2}}}{2}{e^3}$ | C. | $\frac{{\sqrt{3}}}{2}{e^3}$ | D. | e3 |
10.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{3}(x+1),x>0}\\{2f(x+10),x≤0}\end{array}\right.$,则f(-2)等于( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.已知F1,F2是椭圆和双曲线的公共焦点,P是它们的一个公共点,且$∠{F_1}P{F_2}=\frac{π}{3}$,则椭圆和双曲线离心率倒数之和的最大值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{{4\sqrt{3}}}{3}$ | C. | 4 | D. | $\frac{{4\sqrt{6}}}{3}$ |
14.函数f(x)=$\frac{1}{4}$sinxcosx是( )
| A. | 最小正周期为2π的偶函数 | B. | 最小正周期为2π的奇函数 | ||
| C. | 最小正周期为π的偶函数 | D. | 最小正周期为π的奇函数 |

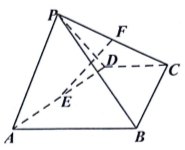 如图,在四棱锥P-ABCD中,△PAD为正三角形,四边形ABCD为直角梯形,CD∥AB,BC⊥AB,平面PAD⊥平面ABCD,点E、F分别为AD、CP的中点,AD=AB=2CD=2.
如图,在四棱锥P-ABCD中,△PAD为正三角形,四边形ABCD为直角梯形,CD∥AB,BC⊥AB,平面PAD⊥平面ABCD,点E、F分别为AD、CP的中点,AD=AB=2CD=2.