题目内容
已知函数y=f（x）在点（2，1）处的切线与直线3x-y-2=0平行，则y′|x=2等于（ ）
| A、-3 | B、-1 | C、3 | D、1 |
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：函数y=f（x）在点（2，1）处的切线斜率等于函数在点（2，1）处的导数值．
解答：
解：函数y=f（x）在点（2，1）处的切线斜率等于函数在点（2，1）处的导数值．
∵函数y=f（x）在点（2，1）处的切线与直线3x-y-2=0平行，
∴y′|x=2=3．
故选：C．
∵函数y=f（x）在点（2，1）处的切线与直线3x-y-2=0平行，
∴y′|x=2=3．
故选：C．
点评：本题考查导数的几何意义，正确理解导数的几何意义是关键．
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
已知点P（sin
，cos
）落在角θ的终边上，且θ∈[0，2π），则tan（θ+
）的值为（ ）
| 3π |
| 4 |
| 3π |
| 4 |
| π |
| 3 |
A、
| ||
B、
| ||
C、2+
| ||
D、2-
|
点P在曲线y=
x3-
x+
上移动，设动点P处的切线的倾斜角为α，则α的取值范围是（ ）
| 1 |
| 3 |
| ||
| 3 |
| 3 |
| 4 |
| A、[0，π] | ||||||
B、（0，
| ||||||
C、[0，
| ||||||
D、[0，
|
函数f（x）=2x的反函数y=f-1（x）的图象是（ ）
A、 |
B、 |
C、 |
D、 |
复数z=
+2i的模为（ ）
| 5-3i |
| 1-i |
| A、3 | ||
| B、4 | ||
| C、5 | ||
D、4
|
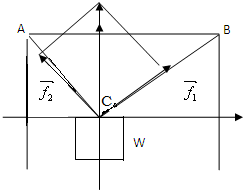物体W的质量为50千克，用绳子将物体W悬挂在两面墙之间，已知两面墙之间的距离AB=10米（AB为水平线），AC=6米，BC=8米，求AC，BC上所受的力的大小．