题目内容
7.f(x)=sin(x-α),f(x)在〔0,$\frac{π}{3}$〕上的定积分等于0,则tanα=( )| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | $\frac{1}{{\sqrt{3}}}$ | D. | -$\frac{1}{{\sqrt{3}}}$ |
分析 利用定积分的运算,求出α的值,再求tanα.
解答 解:${∫}_{0}^{\frac{π}{3}}f(x)dx$=${∫}_{0}^{\frac{π}{3}}sin(x-α)dx$=-[cos(x-α]${丨}_{0}^{\frac{π}{3}}$=0,
∴cosα-cos($\frac{π}{3}$-α)=0,
α=$\frac{π}{3}-α$,
$α=\frac{π}{6}$,
∴tanα=$\frac{1}{\sqrt{3}}$,
故答案选:C
点评 本题考查定积分的计算,属于基础题.

练习册系列答案
相关题目
17.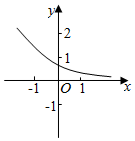 函数f(x)=ax-b的图象如图,其中a,b为常数,则下列结论正确的是( )
函数f(x)=ax-b的图象如图,其中a,b为常数,则下列结论正确的是( )
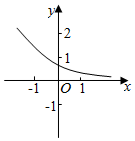 函数f(x)=ax-b的图象如图,其中a,b为常数,则下列结论正确的是( )
函数f(x)=ax-b的图象如图,其中a,b为常数,则下列结论正确的是( )| A. | a>1,b<0 | B. | a>1,b>0 | C. | 0<a<1,b>0 | D. | 0<a<1,b<0 |
2.已知直线l1:3x+4y-3=0,直线l2:6x+8y-1=0平行,则它们之间的距离为( )
| A. | 2 | B. | $\frac{1}{5}$ | C. | $\frac{1}{2}$ | D. | 1 |
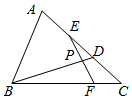 如图,在△ABC中,D、E分别是AB的两个三等分点,F在BC边上,且$\overrightarrow{BF}$=2$\overrightarrow{FC}$,EF与BD交于点P,则$\frac{|BP|}{|PD|}$=( )
如图,在△ABC中,D、E分别是AB的两个三等分点,F在BC边上,且$\overrightarrow{BF}$=2$\overrightarrow{FC}$,EF与BD交于点P,则$\frac{|BP|}{|PD|}$=( )