题目内容
在△ABC的边AB上随机取一点P,记△CAP和△CBP的面积分别为S1和S2,则S1>2S2的概率是 .
考点:几何概型
专题:概率与统计
分析:由S1>2S2,可得AP>2BP,以长度为测度,即可求得概率.
解答:
解:由题意,设AB边上的高为h,
则S1=
•AP•h,S2=
•BP•h,
∵S1>2S2,
∴AP>2BP,
∴S1>2S2的概率是
.
故答案为:
.
则S1=
| 1 |
| 2 |
| 1 |
| 2 |
∵S1>2S2,
∴AP>2BP,
∴S1>2S2的概率是
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查概率的计算,考查三角形面积的计算,确定AP>2BP,以长度为测度是解题的关键.

练习册系列答案
相关题目
下列函数中最小正周期为
的是( )
| π |
| 2 |
| A、y=|sin4x| | ||
B、y=sinxcos(x+
| ||
| C、y=sin(cosx) | ||
| D、y=sin4x+cos2x |
下列四个函数中,以π为最小正周期,且在区间(
,π)上为减函数的是( )
| π |
| 2 |
| A、y=2|sinx| |
| B、y=sin2x |
| C、y=2|cosx| |
| D、y=cos2x |
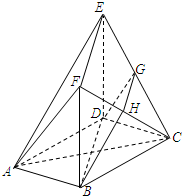 如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE和CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE和CF的中点.