题目内容
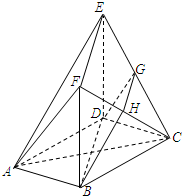 如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE和CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE和CF的中点.(Ⅰ)求证:AC⊥平面BDEF;
(Ⅱ)求证:平面BDGH∥平面AEF;
(Ⅲ)求多面体ABCDEF的体积.
考点:组合几何体的面积、体积问题,平面与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(I)由面面垂直的性质可证AC与平面BDEF垂直;
(II)利用线线平行证明GH∥平面AEF,OH∥平面AEF.由面面平行的判定定理可证面面平行;
(III)把多面体分割成四棱锥A-BDEF和四棱锥C-BDEF,分别求出体积,再求和.
(II)利用线线平行证明GH∥平面AEF,OH∥平面AEF.由面面平行的判定定理可证面面平行;
(III)把多面体分割成四棱锥A-BDEF和四棱锥C-BDEF,分别求出体积,再求和.
解答:
解:(Ⅰ)证明:∵四边形ABCD是正方形,
∴AC⊥BD.
又∵平面BDEF⊥平面ABCD,平面BDEF∩平面ABCD=BD,
且AC?平面ABCD,
∴AC⊥平面BDEF;
(Ⅱ)证明:在△CEF中,
∵G、H分别是CE、CF的中点,
∴GH∥EF,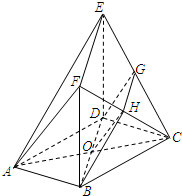
又∵GH?平面AEF,EF?平面AEF,
∴GH∥平面AEF,
设AC∩BD=O,连接OH,在△ACF中,
∵OA=OC,CH=HF,
∴OH∥AF,
又∵OH?平面AEF,AF?平面AEF,
∴OH∥平面AEF.
又∵OH∩GH=H,OH、GH?平面BDGH,
∴平面BDGH∥平面AEF.
(Ⅲ)由(Ⅰ),得 AC⊥平面BDEF,
又∵AO=
,四边形BDEF的面积S=3×2
=6
,
∴四棱锥A-BDEF的体积V1=
×AO×S=4,
同理,四棱锥C-BDEF的体积V2=4.
∴多面体ABCDEF的体积V=8.
∴AC⊥BD.
又∵平面BDEF⊥平面ABCD,平面BDEF∩平面ABCD=BD,
且AC?平面ABCD,
∴AC⊥平面BDEF;
(Ⅱ)证明:在△CEF中,
∵G、H分别是CE、CF的中点,
∴GH∥EF,

又∵GH?平面AEF,EF?平面AEF,
∴GH∥平面AEF,
设AC∩BD=O,连接OH,在△ACF中,
∵OA=OC,CH=HF,
∴OH∥AF,
又∵OH?平面AEF,AF?平面AEF,
∴OH∥平面AEF.
又∵OH∩GH=H,OH、GH?平面BDGH,
∴平面BDGH∥平面AEF.
(Ⅲ)由(Ⅰ),得 AC⊥平面BDEF,
又∵AO=
| 2 |
| 2 |
| 2 |
∴四棱锥A-BDEF的体积V1=
| 1 |
| 3 |
同理,四棱锥C-BDEF的体积V2=4.
∴多面体ABCDEF的体积V=8.
点评:本题考查了面面垂直的性质,面面平行的判定,考查了用分割法求多面体的体积,考查了学生的空间想象能力与推理论证能力.

练习册系列答案
相关题目
设函数f(x)=(
)2x2-5x+b,g(x)=(
)x2+x+6,若f(x)<g(x)对于任意实数x恒成立,则实数b的取值范围是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、b>12 | B、b<12 |
| C、b<15 | D、b>15 |
直线x=1的倾斜角和斜率分别是( )
| A、90°,不存在 |
| B、45°,1 |
| C、135°,-1 |
| D、180°,不存在 |
下列各函数中,是指数函数的是( )
| A、y=(-3)x |
| B、y=-3x |
| C、y=3x-1 |
| D、y=3x |