题目内容
正三棱锥的侧面与底面所成二面角的大小为α，侧棱与底面所成的角为β，则
= ．
| tanα |
| tanβ |
考点：二面角的平面角及求法
专题：空间角
分析：首先利用正三棱锥的性质求出线面垂直，进一步求出线面的夹角和面面的夹角，利用解直角三角形知识求出结果．
解答：
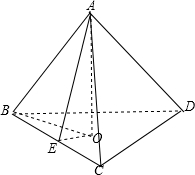解：在正三棱锥A-BCD中，过A做下底面的垂线AO
所以，O为下底面的中心．
做BC的中点E，
所以：OE⊥BC
又由于：AO⊥BC
OE⊥BC
所以：BC⊥平面AOE
则：AE⊥BC
所以：∠AEO即为正三棱锥的侧面与底面所成二面角的大小为α．
连接OB，由于AO⊥平面BCD
所以：∠ABO侧棱与底面所成的角为β．
tanα=
，tanβ=
，
所以：
=
=2
解：在正三棱锥A-BCD中，过A做下底面的垂线AO所以，O为下底面的中心．
做BC的中点E，
所以：OE⊥BC
又由于：AO⊥BC
OE⊥BC
所以：BC⊥平面AOE
则：AE⊥BC
所以：∠AEO即为正三棱锥的侧面与底面所成二面角的大小为α．
连接OB，由于AO⊥平面BCD
所以：∠ABO侧棱与底面所成的角为β．
tanα=
| AO |
| EO |
| AO |
| BO |
所以：
| tanα |
| tanβ |
| BO |
| EO |
点评：本题考查的知识要点：线面的夹角和面面的夹角的应用，正三棱锥的有关问题，属于基础题型．
练习册系列答案
相关题目
已知sinα=2cosα，则
的值为（ ）
| sinα+cosα |
| sinα-cosα |
| A、3 | B、-3 | C、2 | D、-2 |
如图，四棱锥P-ABCD的底面ABCD是矩形，侧面PAB是正三角形，AB=2，BC=已知函数f（x）=
，若关于x的方程f（x）=kx（x∈R）恰有两个不同的实数根，则k的取值范围为（ ）
|
A、k≤0或
| ||
| B、k=1或k≤0 | ||
C、
| ||
D、k≤0或
|