题目内容
已知圆O:x2+y2=4,若焦点在x轴上的椭圆过点P(0,-1),且其长轴长等于圆O的直径,过点P作两条互相垂直的直线l1与l2,l1与⊙O交于A,B两点,l2交椭圆于另一点C.
(1)设直线l1的斜率为k,求弦AB的长;
(2)求△ABC面积的最大值.
(1)设直线l1的斜率为k,求弦AB的长;
(2)求△ABC面积的最大值.
考点:圆与圆锥曲线的综合,直线与圆相交的性质
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意可得b=1,2a=4,即可得到椭圆的方程;由题意可知:直线l1的斜率存在,设为k,则直线l1的方程为y=kx+1.利用点到直线的距离公式和弦长公式即可得出圆心O到直线l1的距离和弦长|AB|;
(2)设A(x1,y1),B(x2,y2),D(x0,y0).根据l2⊥l1,可得直线l2的方程为x+ky-k=0,与椭圆的方程联立即可得到点C的横坐标,即可得出|PC|,即可得到三角形ABC的面积,利用基本不等式的性质即可得出其最大值.
(2)设A(x1,y1),B(x2,y2),D(x0,y0).根据l2⊥l1,可得直线l2的方程为x+ky-k=0,与椭圆的方程联立即可得到点C的横坐标,即可得出|PC|,即可得到三角形ABC的面积,利用基本不等式的性质即可得出其最大值.
解答:
解:(1)由题意,a=2,b=1,∴椭圆的方程为
+y2=1;由题意可知:直线l1的斜率存在,设为k,则直线l1的方程为y=kx-1.
又圆O:x2+y2=4的圆心O(0,0)到直线l1的距离d=
.
∴|AB|=2
=2
.
(Ⅱ)设A(x1,y1),B(x2,y2),C(x0,y0).
∵l2⊥l1,∴直线l2的方程为x+ky+k=0,与椭圆方程联立联立,
消去y得到(4+k2)x2+8kx=0,解得x0=-
,
∴|PC|=
.
∴三角形ABC的面积S△=
|AB|•|PD|=
=
≤
=
,
当且仅当k=±
时取等号,
故所求直线l1的方程为y=±
x-1,此时△ABC面积的最大值为
.
| x2 |
| 4 |
又圆O:x2+y2=4的圆心O(0,0)到直线l1的距离d=
| 1 | ||
|
∴|AB|=2
| 4-d2 |
|
(Ⅱ)设A(x1,y1),B(x2,y2),C(x0,y0).
∵l2⊥l1,∴直线l2的方程为x+ky+k=0,与椭圆方程联立联立,
消去y得到(4+k2)x2+8kx=0,解得x0=-
| 8k |
| 4+k2 |
∴|PC|=
8
| ||
| 4+k2 |
∴三角形ABC的面积S△=
| 1 |
| 2 |
8
| ||
| 4+k2 |
| 32 | ||||||
|
| 32 | ||
2
|
16
| ||
| 13 |
当且仅当k=±
| ||
| 2 |
故所求直线l1的方程为y=±
| ||
| 2 |
16
| ||
| 13 |
点评:本题主要考查了椭圆的几何性质、直线与圆及椭圆的位置关系的综合应用,同时考查了推理能力和计算能力及分析问题和解决问题的能力

练习册系列答案
相关题目
在等差数列{an}中,已知a5+a7=16,则该数列前11项和S11的值是( )
| A、88 | B、58 |
| C、143 | D、176 |
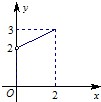 已知函数f(x)是定义在[-2,0)∪(0,2]上的奇函数,当x>0时,f(x)的图象如图所示.
已知函数f(x)是定义在[-2,0)∪(0,2]上的奇函数,当x>0时,f(x)的图象如图所示.