题目内容
9．随机变量ξ服从二项分布ξ～B（n，p），且Eξ=300，Dξ=200，则p等于（ ）| A． | $\frac{2}{3}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
分析 利用期望与方差列出方程，求解即可．
解答 解：随机变量ξ服从二项分布ξ～B（n，p），且Eξ=300，Dξ=200，
可得：np=300，np（1-p）=200，
解得p=$\frac{1}{3}$．
故选：B．
点评 本题考查二项分布的期望与方差的求法，考查计算能力．
练习册系列答案
相关题目
20．在直角坐标系中，点A（1，-2），B（-2，2），则A，B两点间的距离为（ ）
| A． | $\sqrt{14}$ | B． | 5 | C． | $\sqrt{31}$ | D． | 25 |
17．已知sin（π+α）-3cos（2π-α）=0，则cos2α的值为（ ）
| A． | $\frac{4}{5}$ | B． | -$\frac{4}{5}$ | C． | $\frac{3}{5}$ | D． | -$\frac{3}{5}$ |
4．随机变量X的分布列如下：
若EX=$\frac{1}{3}$，则DX的值是（ ）
| X | -1 | 0 | 1 |
| P | a | $\frac{1}{3}$ | b |
| A． | $\frac{1}{9}$ | B． | $\frac{2}{9}$ | C． | $\frac{4}{9}$ | D． | $\frac{5}{9}$ |
（
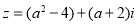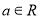），则“
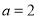”是“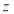
为纯虚数”的（ ）