题目内容
已知数列{an}的前n项和Sn=
n(n+1),n∈N*,bn=3an+(-1)n-1an,则数列{bn}的前2n+1项和为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:数列递推式,数列的求和
专题:等差数列与等比数列
分析:由数列的前n项和求出数列{an}的通项公式,代入bn=3an+(-1)n-1an,整理后分组,然后利用等比数列的前n项和得答案.
解答:
解:当n=1时,a1=S1=
×1×2=1;
当n≥2时,an=Sn-Sn-1=
n(n+1)-
(n-1)n=n.
故an=n.
∴bn=3an+(-1)n-1an=3n+(-1)n-1n,
则数列{bn}的前2n+1项和S2n+1=(31+32+…+32n+1)+[1-2+3-4+…+(2n-1)-2n+(2n+1)]
=
+(n+1)=
+n.
故选:A.
| 1 |
| 2 |
当n≥2时,an=Sn-Sn-1=
| 1 |
| 2 |
| 1 |
| 2 |
故an=n.
∴bn=3an+(-1)n-1an=3n+(-1)n-1n,
则数列{bn}的前2n+1项和S2n+1=(31+32+…+32n+1)+[1-2+3-4+…+(2n-1)-2n+(2n+1)]
=
| 3(1-32n+1) |
| 1-3 |
| 32n+2-1 |
| 2 |
故选:A.
点评:本题考查了数列递推式,考查了数列的分组求和,考查了等比数列的前n项和,是中档题.

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
已知向量
=(sin(
-α),sinα),
=(sin(
+β),sinβ),且0<β<α<π,向量
=(cos
,sin
),
=(sinπ,sin
),若
+
=
+
,则以下说法正确的是( )
| a |
| π |
| 2 |
| b |
| π |
| 2 |
| c |
| π |
| 2 |
| π |
| 3 |
| d |
| 2π |
| 3 |
| a |
| b |
| c |
| d |
| A、sinα>sinβ |
| B、cos(α-β)=1 |
| C、α+β>π |
| D、sinα<tanβ |


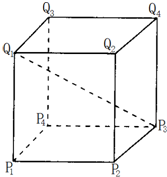 若正方体P1P2P3P4-Q1Q2Q3Q4的棱长为1,
若正方体P1P2P3P4-Q1Q2Q3Q4的棱长为1,