Question

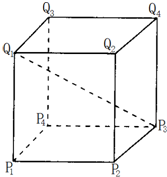若正方体P₁P₂P₃P₄-Q₁Q₂Q₃Q₄的棱长为1，
集合M={x|x=

P1Q1

•

SiTj

，S，T∈{P，Q}，i，j∈{1，2，3，4}}，
则对于下列结论：
①当

SiTj

=

PiQj

时，x=1；
②当

SiTj

=

QiPj

时，x=1；
③当x=1时，（i，j）有16种不同取值；
④M={-1，0，1}
其中正确的结论序号为

 

（填上所有正确结论的序号）．

Answer 1

考点：命题的真假判断与应用

专题：综合题,推理和证明

分析：根据题意，建立空间直角坐标系，得出向量

PiQj

，

P1Q1

，

PiPj

，

QiPj

的坐标表示，求出x=

P1Q1

•

SiTj

的值即可判断所给的结论是否正确．

解答： 解：根据题意，建立空间直角坐标系，如图所示；
①当

SiTj

=

PiQj

时，x=

P1Q1

•

PiQj

=（0，0，1）•（x_i，x_j，1）=1，
∴①正确；
②当

SiTj

=

QiPj

时，由①知，x=-1，∴②错误；
③当x=1时，i=1、2、3、4，j=1、2、3、4，（i，j）有4×4=16种不同的取值，∴③正确；
④当

SiTj

=

PiQj

时，x=

P1Q1

•

PiQj

=1，
当

SiTj

=

PiPj

时，x=

P1Q1

•

PiQj

=（0，0，1）•（x_i，x_j，0）=0，
当

SiTj

=

QiPj

时，x=

P1Q1

•

QiPj

=（0，0，1）•（x_i，x_j，-1）=-1，
∴M={-1，0，1}，④正确．
综上，正确的结论是①③④．
故答案为：①③④．

点评：本题考查了空间向量的应用问题，也考查了集合知识的应用问题，是综合性题目．