题目内容
如图是某市今年1月份前30天空气质量指数(AQI)的趋势图.

(1)根据该图数据在答题卷中完成频率分布表,并在图3中作出这些数据的频率分布直方图;
(2)当空气质量指数(AQI)小于100时,表示空气质量优良.某人随机选择当月1日至10日中的某一天到达该市,并停留2天,设ξ是此人停留期间空气质量优良的天数,求ξ的数学期望.

(图中纵坐标1/300即
,以此类推)

(1)根据该图数据在答题卷中完成频率分布表,并在图3中作出这些数据的频率分布直方图;
| 分组 | 频数 | 频率 |
| [20,40) | ||
| [40,60) | ||
| [60,80) | ||
| [80,100) | ||
| [100,120) | ||
| [120,140) | ||
| [140,160) | ||
| [160,180) | ||
| [180.200] | ||
| 合计 | 30 | 1 |

(图中纵坐标1/300即
| 1 |
| 300 |
考点:频率分布直方图
专题:应用题,概率与统计
分析:(1)根据图中数据,列出频率分布表,画出频率分布直方图即可;
(2)设Ai表示事件“此人于当月i日到达该市”,得出P(Ai),计算P(ξ)的值,求出ξ的数学期望Eξ.
(2)设Ai表示事件“此人于当月i日到达该市”,得出P(Ai),计算P(ξ)的值,求出ξ的数学期望Eξ.
解答:
解:(1)根据图中数据,列出频率分布表如下;
根据频率分布表,画出频率分布直方图,如下;

(2)设Ai表示事件“此人于当月i日到达该市”( i=1,2,…,10);
则P(Ai)=
( i=1,2,…,10),
依题意可知,ξ的所有可能取值为0,1,2,且
P(ξ=0)=P(A5)+P(A6)=
=
,
P(ξ=1)=P(A1)+P(A4)+P(A7)+P(A10)=
=
,
P(ξ=2)=P(A2)+P(A3)+P(A8)+P(A9)=
=
,
所以ξ的数学期望为Eξ=0×
+1×
+2×
=
.
| 分组 | 频数 | 频率 | ||
| [20,40) | 2 |
| ||
| [40,60) | 5 |
| ||
| [60,80) | 7 |
| ||
| [80,100) | 5 |
| ||
| [100,120) | 2 |
| ||
| [120,140) | 5 |
| ||
| [140,160) | 1 |
| ||
| [160,180) | 1 |
| ||
| [180.200] | 2 |
| ||
| 合计 | 30 | 1 |

(2)设Ai表示事件“此人于当月i日到达该市”( i=1,2,…,10);
则P(Ai)=
| 1 |
| 10 |
依题意可知,ξ的所有可能取值为0,1,2,且
P(ξ=0)=P(A5)+P(A6)=
| 2 |
| 10 |
| 1 |
| 5 |
P(ξ=1)=P(A1)+P(A4)+P(A7)+P(A10)=
| 4 |
| 10 |
| 2 |
| 5 |
P(ξ=2)=P(A2)+P(A3)+P(A8)+P(A9)=
| 4 |
| 10 |
| 2 |
| 5 |
所以ξ的数学期望为Eξ=0×
| 1 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 6 |
| 5 |
点评:本题考查了频率分布直方图的应用问题,也考查了求随机变量的数学期望的应用问题,是基础题目.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
已知y=f(x)是定义在R上的函数,下列命题正确的是( )
| A、若f(x)在区间[a,b]上的图象是一条连续不断的曲线,且在(a,b)内有零点,则有f(a)•f(b)<0 |
| B、若f(x)在区间[a,b]上的图象是一条连续不断的曲线,且有f(a)•f(b)>0,则其在(a,b)内没有零点 |
| C、若f(x)在区间(a,b)上的图象是一条连续不断的曲线,且有f(a)•f(b)<0,则其在(a,b)内有零点 |
| D、如果函数f(x)在区间[a,b]上的图象是一条连续不断的曲线,且有f(a)•f(b)<0,则其在(a,b)内有零点 |
执行图中的程序框图(其中[x]表示不超过x的最大整数),则输出的S值为( )


| A、4 | B、5 | C、6 | D、7 |
若二项式(x+
)7的展开式中
的系数与
的系数之比是35:21,则a=( )
| a |
| x |
| 1 |
| x |
| 1 |
| x3 |
| A、1 | B、2 | C、-1 | D、-2 |
已知数列{an}的前n项和Sn=
n(n+1),n∈N*,bn=3an+(-1)n-1an,则数列{bn}的前2n+1项和为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 在多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2AB,F为棱CE上异于点C、E的动点,则下列说法正确的有( )
在多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2AB,F为棱CE上异于点C、E的动点,则下列说法正确的有( )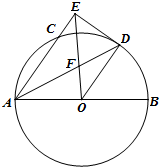 如图,已知AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线AD交⊙O于D,过点D作DE⊥AC交AC的延长线于点E,OE交AD于点F.若
如图,已知AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线AD交⊙O于D,过点D作DE⊥AC交AC的延长线于点E,OE交AD于点F.若