题目内容
已知直线l经过点P(-2,5),且斜率为-
.
(Ⅰ)求直线l的方程;
(Ⅱ)若直线m与l平行,且点P到直线m的距离为3,求直线m的方程.
| 3 |
| 4 |
(Ⅰ)求直线l的方程;
(Ⅱ)若直线m与l平行,且点P到直线m的距离为3,求直线m的方程.
考点:直线的一般式方程与直线的平行关系,直线的点斜式方程
专题:直线与圆
分析:(1)由已知条件,直接利用直线方程的点斜式能得到所求直线方程.
(2)由直线m与直线l平行,可设直线m的方程为3x+4y+C=0,再由点到直线的距离公式求出C,从而求出所求直线方程.
(2)由直线m与直线l平行,可设直线m的方程为3x+4y+C=0,再由点到直线的距离公式求出C,从而求出所求直线方程.
解答:
解:(1)由直线方程的点斜式,
得y-5=-
(x+2),…(2分)
整理得所求直线方程为:
3x+4y-14=0.…(4分)
(2)由直线m与直线l平行,可设直线m的方程为3x+4y+C=0,…(6分)
由点到直线的距离公式得
=3,…(8分)
即
=3,
解得C=1或C=-29,…(10分)
故所求直线方程为
3x+4y+1=0或3x+4y-29=0.…(12分)
得y-5=-
| 3 |
| 4 |
整理得所求直线方程为:
3x+4y-14=0.…(4分)
(2)由直线m与直线l平行,可设直线m的方程为3x+4y+C=0,…(6分)
由点到直线的距离公式得
| |3×(-2)+4×5+C| | ||
|
即
| |14+C| |
| 5 |
解得C=1或C=-29,…(10分)
故所求直线方程为
3x+4y+1=0或3x+4y-29=0.…(12分)
点评:本题考查直线方程的求法,是基础题,涉及到直线的点斜式方程、直线平行的条件、点到直线距离公式等知识点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(理科)已知满足条件x2+y2≤1的点(x,y)构成的平面区域的面积为S1,满足条件[x]2+[y]2≤1的点(x,y)构成的平面区域的面积为S2,(其中[x]、[y]分别表示不大于x、y的最大整数),则下列关系正确的是( )
| A、S1=S2 |
| B、S1>S2 |
| C、S1<S2 |
| D、S22+S12=π2 |
下列哪个函数与y=x是同一个函数的是( )
| A、y=|x| | ||
B、y=
| ||
C、y=(
| ||
| D、y=t |
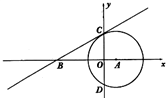 已知:如图,⊙A与y轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为
已知:如图,⊙A与y轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为