Question

在正方体ABCD-A₁B₁C₁D₁中，B₁C与对角面DD₁B₁B所成角的大小是

 

．

Answer 1

考点：直线与平面所成的角

专题：空间角

分析：建立空间直角坐标系，求出

BC1

=（-2，0，2），

AC

=（-2，2，0），

AC

且为平面BB₁D₁D的一个法向量，利用向量的夹角公式，可求BC₁与平面BB₁D₁D所成角的正弦值，即可得出结论．

解答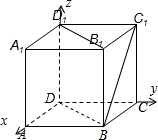： 解：以D点为坐标原点，以DA、DC、DD₁所在的直线为x轴、y轴、z轴，建立空间直角坐标系，
则A（2，0，0），B（2，2，0），C（0，2，0），C₁（0，2，2）
∴

BC1

=（-2，0，2），

AC

=（-2，2，0），

AC

且为平面BB₁D₁D的一个法向量．
∴cos＜

BC1

，

AC

＞=

4

2 2 •2 2

=

1

2

，
∴BC₁与平面BB₁D₁D所成角的正弦值为

1

2

，
∴BC₁与平面BB₁D₁D所成角为30°．
故答案为：30°．

点评：本题主要考查了直线与平面之间所成角，重点考查了利用空间向量，抓住直线与平面所成的角与该直线的方向向量与平面的法向量的夹角之间的关系是解题的关键．