题目内容
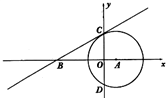 已知:如图,⊙A与y轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为
已知:如图,⊙A与y轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为| 5 |
(1)求切线BC的解析式;
(2)若点P是第一象限内⊙A上的一点,过点P作⊙A的切线与直线BC相交于点G,且∠CGP=120°,求点G的坐标.
(3)向左移动⊙A(圆心A始终保持在x轴上),与直线BC交于E、F,在移动过程中是否存在点A,使△AEF是直角三角形?若存在,求出点A的坐标;若不存在,请说明理由.
考点:直线和圆的方程的应用
专题:直线与圆
分析:(1)根据直线与圆相切的性质可求出BC的方程.
(2)过G作x轴的垂线,垂足为H,连结AG,先求出OH,即G点的横坐标,然后代入直线BC的方程,即可求出;
(3)假设存在,根据直线与圆相交的性质解决.
(2)过G作x轴的垂线,垂足为H,连结AG,先求出OH,即G点的横坐标,然后代入直线BC的方程,即可求出;
(3)假设存在,根据直线与圆相交的性质解决.
解答:
 (1)由题意可知,圆的方程是(x-1)2+y2=5
(1)由题意可知,圆的方程是(x-1)2+y2=5
将y=0代入圆的方程得
点C的坐标为(0,2),
∵kAC=-2,
∴kBC=-
得出直线的解析式为y=
x+2;
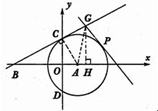
(2)如图:过G作x轴的垂线,垂足为H,连结AG,
设G(x0,y0),在Rt△ACG中,∠ACG=90°,AC=
,
求得CG=
,
又由OB=4,BC=
=2
,
由CO∥GH,
得
=
,
则OH=
,即x0=
.
又点G在直线BC上,
∴y0=
×
+2=
,
∴G(
,
)
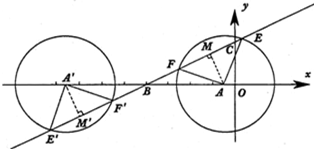
(3)如图:在移动过程中,存在点A,使△AEF为直角三角形.
理由:由题意得△AEF是等腰三角形,
∴只能是∠EAF=90°,
∴△AEF是以EF为斜边的等腰直角三角形.
过点A作AM⊥EF于点M,
则AM=
EF=
.
由△BAM≌△BCO得
=
,
设A(a,0),则BA=a+4,BC=2
,OC=2,AM=
可得出a=
,
∴A(
,0).
同理当BA=-4-a,BC=2
,OC=2,
可得出a=-
,∴A′(-
,0).
∴存在两个点使△AEF为直角三角形.它的坐标是A(
,0),A′(-
,0).

 (1)由题意可知,圆的方程是(x-1)2+y2=5
(1)由题意可知,圆的方程是(x-1)2+y2=5将y=0代入圆的方程得
点C的坐标为(0,2),
∵kAC=-2,
∴kBC=-
| 1 |
| 2 |
得出直线的解析式为y=
| 1 |
| 2 |
(2)如图:过G作x轴的垂线,垂足为H,连结AG,
设G(x0,y0),在Rt△ACG中,∠ACG=90°,AC=
| 5 |
求得CG=
| ||
| 3 |
又由OB=4,BC=
| OB2+OC2 |
| 5 |
由CO∥GH,
得
| OH |
| BO |
| CG |
| BC |
则OH=
2
| ||
| 3 |
2
| ||
| 3 |
又点G在直线BC上,
∴y0=
| 1 |
| 2 |
2
| ||
| 3 |
| ||
| 3 |
∴G(
2
| ||
| 3 |
| ||
| 3 |
(3)如图:在移动过程中,存在点A,使△AEF为直角三角形.
理由:由题意得△AEF是等腰三角形,
∴只能是∠EAF=90°,
∴△AEF是以EF为斜边的等腰直角三角形.
过点A作AM⊥EF于点M,
则AM=
| 1 |
| 2 |
| ||
| 2 |
由△BAM≌△BCO得
| BA |
| BC |
| AM |
| OC |
设A(a,0),则BA=a+4,BC=2
| 5 |
| ||
| 2 |
可得出a=
5
| ||
| 2 |
∴A(
5
| ||
| 2 |
同理当BA=-4-a,BC=2
| 5 |
可得出a=-
5
| ||
| 2 |
5
| ||
| 2 |
∴存在两个点使△AEF为直角三角形.它的坐标是A(
5
| ||
| 2 |
5
| ||
| 2 |
点评:本题考查了直线与圆的位置关系,两直线垂直的性质,直角三角形勾股定理等知识的综合应用.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
已知等差数列{an}中,an=4n-3,则首项a1和公差d的值分别为( )
| A、1,3 | B、-3,4 |
| C、1,4 | D、1,2 |