题目内容
一艘渔艇停泊在距岸9km处，今需派人送信给距渔艇3
km处的海岸渔站中，如果送信人步行每小时5km，船速每小时4km，问应在何处登岸可以使抵达渔站的时间最省？
| 34 |
考点：导数在最大值、最小值问题中的应用
专题：导数的综合应用
分析：先求出时间的表达式，再利用导数的方法求出最值即可．
解答：
解：如图，设渔艇停泊在A处，
海岸线BC（C为渔站），AB⊥BC于B．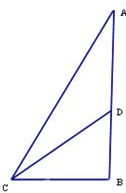
∴AB=9，AC=3
．
设此人在D处登岸，CD=x，
则BC=
=15，
∴BD=15-x，∴AD=
，
∴送信所需时间t=
+
，
∴t′=
+
=
．
令t'=0时，解得（5x-75）2=16[81+（15-x）2]．
∴|15-x|=12，∴x=3，x=27（舍去）．
答：此人在距渔站3km处登岸可使抵达渔站的时间最短．
海岸线BC（C为渔站），AB⊥BC于B．
∴AB=9，AC=3
| 34 |
设此人在D处登岸，CD=x，
则BC=
| AC2-AB2 |
∴BD=15-x，∴AD=
| 92+(15-x)2 |
∴送信所需时间t=
| ||
| 4 |
| x |
| 5 |
∴t′=
| -(15-x) | ||
4
|
| 1 |
| 5 |
4
| ||
20
|
令t'=0时，解得（5x-75）2=16[81+（15-x）2]．
∴|15-x|=12，∴x=3，x=27（舍去）．
答：此人在距渔站3km处登岸可使抵达渔站的时间最短．
点评：本题考查函数模型的构建，考查导数知识的运用，考查利用数学知识解决实际问题，属于中档题．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知sinα+cosα=
，则cos（
+2α）等于（ ）
| 3 |
| 5 |
| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|