题目内容
已知数列{an}是等比数列,且Sm=10,S2m=30,则S3m为( )
| A、90 | B、70 | C、50 | D、80 |
考点:等比数列的前n项和
专题:等差数列与等比数列
分析:由已知数据可得S2m-Sm=20,再由Sm,S2m-Sm,S3m-S2m成等比数列,计算可得答案.
解答:
解:由等比数列的性质可得Sm,S2m-Sm,S3m-S2m成等比数列,
∵Sm=10,S2m=30,
∴S2m-Sm=20,
∴S3m-S2m=40,
∴S3m=30+40=70,
故选:B.
∵Sm=10,S2m=30,
∴S2m-Sm=20,
∴S3m-S2m=40,
∴S3m=30+40=70,
故选:B.
点评:本题考查等比数列的性质,利用Sm,S2m-Sm,S3m-S2m成等比数列是解决问题的关键,属基础题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
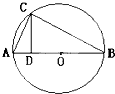 如图,圆的直径AB=13cm,C为圆上的一点,CD⊥AB,垂足为D,且CD=6cm,则AD的长是( )
如图,圆的直径AB=13cm,C为圆上的一点,CD⊥AB,垂足为D,且CD=6cm,则AD的长是( )| A、4 | B、9 | C、4或9 | D、6 |
已知变量x与y之间一组对应数据如表格所示,经计算它们的回归直线方程为
=2.3x+0.8,定义ei=yi-
i为第i组数据的残差,如果要去除残差绝对值最大的那组数据,则应该去除( )
 |
| y |
 |
| y |
| 序号i | 1 | 2 | 3 | 4 |
| xi | 0 | 1 | 2 | 3 |
| yi | 1 | 3 | 5 | 8 |
| A、第1组 | B、第2组 |
| C、第3组 | D、第4组 |
在极坐标系中,圆ρ=2cosθ+2sinθ的圆心的极坐标是( )
A、(1,
| ||||
B、(1,
| ||||
C、(
| ||||
D、(
|
已知点P(-1,1)与点Q(3,5)关于直线l对称,则直线l的方程为( )
| A、x-y+1=0 |
| B、x+y=0 |
| C、x+y-4=0 |
| D、x-y=0 |
直线ax+y+1=0与连接A(2,3),B(-3,2)的线段相交,则a的取值范围是( )
| A、[-1,2] |
| B、(-∞,-1]∪[2,+∞) |
| C、[-2,1] |
| D、(-∞,-2]∪[1,+∞) |
直线l过点P(1,3),且与x、y轴正半轴围成的三角形的面积等于6的直线方程是( )
| A、3x+y-6=0 |
| B、x+3y-10=0 |
| C、3x-y=0 |
| D、x-3y+8=0 |
 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC.
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC.