题目内容
已知sinα+cosα=
，且0＜α＜
．
（Ⅰ）求sinαcosα、sinα-cosα的值；
（Ⅱ）求
-
的值．
| 7 |
| 5 |
| π |
| 4 |
（Ⅰ）求sinαcosα、sinα-cosα的值；
（Ⅱ）求
| sin3α |
| 1+tanα |
| sinα•cos3α |
| sinα+cosα |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：（Ⅰ）已知等式两边平方，利用完全平方公式及同角三角函数间基本关系化简，求出sinαcosα的值，再利用完全平方公式变形求出sinα-cosα的值即可；
（Ⅱ）原式利用同角三角函数间的基本关系切化弦后，利用同分母分式的减法法则计算，约分后将各自的值代入计算即可求出值．
（Ⅱ）原式利用同角三角函数间的基本关系切化弦后，利用同分母分式的减法法则计算，约分后将各自的值代入计算即可求出值．
解答：
解：（Ⅰ）∵sinα+cosα=
两边平方得：1+2sinαcosα=
，
∴sinαcosα=
，
∵（sinα-cosα）2=1-2sinαcosα=
，
又∵0＜α＜
，
∴sinα-cosα=-
；
（Ⅱ）∵sinαcosα=
，sinα-cosα=-
，
∴原式=
=
=sinαcosα（sinα-cosα）=-
．
| 7 |
| 5 |
| 49 |
| 25 |
∴sinαcosα=
| 12 |
| 25 |
∵（sinα-cosα）2=1-2sinαcosα=
| 1 |
| 25 |
又∵0＜α＜
| π |
| 4 |
∴sinα-cosα=-
| 1 |
| 5 |
（Ⅱ）∵sinαcosα=
| 12 |
| 25 |
| 1 |
| 5 |
∴原式=
| cosαsin3α-sinαcos3α |
| sinα+cosα |
| sinαcosα(sinα+cosα)(sinα-cosα) |
| sinα+cosα |
| 12 |
| 125 |
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
如图所示，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，点E在线段PC上，PC⊥平面BDE，PA=2，AD=4，二面角B-PC-D的正切值为（ ）A、-
| ||
B、-
| ||
C、-2
| ||
D、-
|
已知数列{an}是等比数列，且Sm=10，S2m=30，则S3m为（ ）
| A、90 | B、70 | C、50 | D、80 |
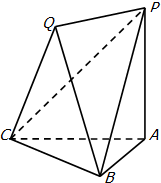（文）在空间几何体PQ-ABC中，PA⊥平面ABC，平面QBC⊥平面ABC，AB=AC，QB=QC．