题目内容
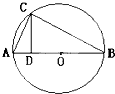如图，圆的直径AB=13cm，C为圆上的一点，CD⊥AB，垂足为D，且CD=6cm，则AD的长是（ ）| A、4 | B、9 | C、4或9 | D、6 |
考点：与圆有关的比例线段
专题：立体几何
分析：由射影定理得CD2=AD•BD，由此能求出AD的长．
解答：
解：∵圆的直径AB=13cm，C为圆上的一点，
CD⊥AB，垂足为D，且CD=6cm，
∴CD2=AD•BD，
即36=AD（13-AD），
整理，得AD2-13AD+36=0，
解得AD=4，或AD=9．
故选：C．
CD⊥AB，垂足为D，且CD=6cm，
∴CD2=AD•BD，
即36=AD（13-AD），
整理，得AD2-13AD+36=0，
解得AD=4，或AD=9．
故选：C．
点评：本题考查与圆有关的线段长的求法，是基础题，解题时要认真审题，注意射影定理的合理运用．
练习册系列答案
相关题目
如图，已知正三角形ABC的边长为6，点D为边AC的中点，点E为边AB上离点A较近的三等分点，则函数y=loga（x-2）+1（a＞0且a≠1）的图象恒过的一个定点是（ ）
| A、（3，0） |
| B、（3，1） |
| C、（2，1） |
| D、（2，2） |
已知直线L：x=my+n（n＞0）过点A（5
，5），若可行域的面积
为25
，则（n+mx）4展开式中系数绝对值得和为（ ）
| 3 |
|
| 3 |
A、（11
| ||
| B、9×114 | ||
| C、9×104 | ||
| D、9×115 |
设s=（x-1）4+4（x-1）3+6（x-1）2+4（x-1）+1，它等于下式中的（ ）
| A、x4 |
| B、（x-1）4 |
| C、（x+1）4 |
| D、（x-2）4 |
已知直线的倾斜角为45°，在y轴上的截距为1，则此直线方程为（ ）
| A、y=-x+1 |
| B、y=x+1 |
| C、y=-x-1 |
| D、y=x-1 |
如图所示，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，点E在线段PC上，PC⊥平面BDE，PA=2，AD=4，二面角B-PC-D的正切值为（ ）A、-
| ||
B、-
| ||
C、-2
| ||
D、-
|
已知数列{an}是等比数列，且Sm=10，S2m=30，则S3m为（ ）
| A、90 | B、70 | C、50 | D、80 |