题目内容
直线ax+y+1=0与连接A(2,3),B(-3,2)的线段相交,则a的取值范围是( )
| A、[-1,2] |
| B、(-∞,-1]∪[2,+∞) |
| C、[-2,1] |
| D、(-∞,-2]∪[1,+∞) |
考点:直线的斜率
专题:直线与圆
分析:由直线ax+y+1=0的方程,判断恒过P(0,-1),求出KPA与KPB,判断过P点的竖直直线与AB两点的关系,求出满足条件的直线斜率的取值范围.
解答:
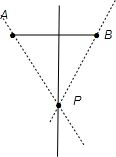 解:由直线ax+y+1=0的方程,判断恒过P(0,-1),
解:由直线ax+y+1=0的方程,判断恒过P(0,-1),
如下图示:
∵KPA=2,KPB=-1,
则实数a的取值范围是:a≤-2或a≥1.
故答案为:a≤-2或a≥1.
 解:由直线ax+y+1=0的方程,判断恒过P(0,-1),
解:由直线ax+y+1=0的方程,判断恒过P(0,-1),如下图示:
∵KPA=2,KPB=-1,
则实数a的取值范围是:a≤-2或a≥1.
故答案为:a≤-2或a≥1.
点评:求恒过P点且与线段AB相交的直线的斜率的取值范围,有两种情况:
当AB,在P竖直方向上的同侧时,(如本题)计算KPA与KPB,若KPA<KPB,则直线的斜率k∈[KPA,KPB]
当AB,在P竖直方向上的异侧时,(如下图)计算KPA与KPB,若KPA<KPB,则直线的斜率k∈(-∞,KPA]∪[KPB,+∞)
就是过p点的垂直x轴的直线与线段有交点时,斜率范围写两段区间,无交点时写一段区间.
当AB,在P竖直方向上的同侧时,(如本题)计算KPA与KPB,若KPA<KPB,则直线的斜率k∈[KPA,KPB]
当AB,在P竖直方向上的异侧时,(如下图)计算KPA与KPB,若KPA<KPB,则直线的斜率k∈(-∞,KPA]∪[KPB,+∞)
就是过p点的垂直x轴的直线与线段有交点时,斜率范围写两段区间,无交点时写一段区间.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设s=(x-1)4+4(x-1)3+6(x-1)2+4(x-1)+1,它等于下式中的( )
| A、x4 |
| B、(x-1)4 |
| C、(x+1)4 |
| D、(x-2)4 |
设s,t是非零实数,
,
是单位向量,当两向量s
+t
,t
-s
的模相等时,
,
的夹角是( )
| i |
| j |
| i |
| j |
| i |
| j |
| i |
| j |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知向量
=(1,k),
=(2,k-3),且
∥
,则k的值为( )
| a |
| b |
| a |
| b |
| A、-3 | B、0 | C、1 | D、3 |
已知数列{an}是等比数列,且Sm=10,S2m=30,则S3m为( )
| A、90 | B、70 | C、50 | D、80 |
圆的极坐标方程分别是ρ=2cosθ和ρ=4sinθ,两个圆的圆心距离是( )
| A、2 | ||
B、
| ||
C、
| ||
| D、5 |