题目内容
 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC.
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC.(1)求证:BE∥平面PDA;
(2)求证:平面PBD⊥平面PBE.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)由已条条件推导出平面BEC∥平面PDA,由此能证明BE∥平面PDA.
(2)连接AC与BD交于点F,连接NF,由已知条件推导出四边形NFCE为平行四边形,由此推导出NE⊥面PDB.从而能证明平面PBD⊥平面PBE.
(2)连接AC与BD交于点F,连接NF,由已知条件推导出四边形NFCE为平行四边形,由此推导出NE⊥面PDB.从而能证明平面PBD⊥平面PBE.
解答:
证明:(1)∵EC∥PD,PD?平面PDA,EC?平面PDA
∴EC∥平面PDA,
同理可得BC∥平面PDA,
∵EC?平面EBC,BC?平面EBC,且EC∩BC=C,
∴平面BEC∥平面PDA,
又∵BE?平面EBC,∴BE∥平面PDA.
(2)连接AC与BD交于点F,连接NF,
∵F为BD的中点,∴NF∥PD,且NF=
PD.
又EC∥PD,且EC=
PD,∴NF∥EC且NF=EC,
∴四边形NFCE为平行四边形,∴NE∥FC.
∵DB⊥AC,PD⊥平面ABCD,AC?面ABCD,∴AC⊥PD,
又PD∩BD=D,∴AC⊥面PBD,∴NE⊥面PDB.
∵NE?平面PBE,∴平面PBD⊥平面PBE.
∴EC∥平面PDA,
同理可得BC∥平面PDA,
∵EC?平面EBC,BC?平面EBC,且EC∩BC=C,

∴平面BEC∥平面PDA,
又∵BE?平面EBC,∴BE∥平面PDA.
(2)连接AC与BD交于点F,连接NF,
∵F为BD的中点,∴NF∥PD,且NF=
| 1 |
| 2 |
又EC∥PD,且EC=
| 1 |
| 2 |
∴四边形NFCE为平行四边形,∴NE∥FC.
∵DB⊥AC,PD⊥平面ABCD,AC?面ABCD,∴AC⊥PD,
又PD∩BD=D,∴AC⊥面PBD,∴NE⊥面PDB.
∵NE?平面PBE,∴平面PBD⊥平面PBE.
点评:本题考查直线与平面平行的证明,考查平面与平面垂直的证明,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
已知数列{an}是等比数列,且Sm=10,S2m=30,则S3m为( )
| A、90 | B、70 | C、50 | D、80 |
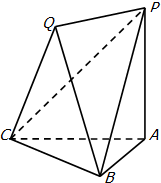 (文)在空间几何体PQ-ABC中,PA⊥平面ABC,平面QBC⊥平面ABC,AB=AC,QB=QC.
(文)在空间几何体PQ-ABC中,PA⊥平面ABC,平面QBC⊥平面ABC,AB=AC,QB=QC.