题目内容
已知函数f(x)=1+lnx+
.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若f(x)>k在x∈(1,+∞)时恒成立,求整数k的最大值.
| k |
| x |
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若f(x)>k在x∈(1,+∞)时恒成立,求整数k的最大值.
考点:导数在最大值、最小值问题中的应用
专题:综合题,导数的综合应用
分析:(Ⅰ)求函数定义域,然后分k≤0,k>0两种1情况讨论,在定义域内解不等式f′(x)>0,f′(x)<0即可;
(Ⅱ)f(x)>k在x∈(1,+∞)时恒成立,等价于f(x)min>k,分k≤1,k>1两种情况讨论,利用(Ⅰ)的结论可求得f(x)min;
(Ⅱ)f(x)>k在x∈(1,+∞)时恒成立,等价于f(x)min>k,分k≤1,k>1两种情况讨论,利用(Ⅰ)的结论可求得f(x)min;
解答:
解:(Ⅰ)f(x)的定义域为(0,+∞),
f′(x)=
-
=
;
①当k≤0时,f′(x)>0,f(x)递增;
②当k>0时,由f′(x)>0,得x>k,由f′(x)<0,得0<x<k;
综上,当k≤0时,f(x)的单调递增区间为(0,+∞);当k>0时,f(x)的单调递减区间为(0,k),单调递增区间为(k,+∞).
(Ⅱ)f(x)>k,
①当k≤1时,由(Ⅰ)知f(x)在(1,+∞)上单调递增,
∴f(x)>f(1)=1+k,则1+k≥k恒成立,
∴此时k≤1;
②当k>1时,由(I)知,f(x)在(1,k)上递减,在(k,+∞)上递增,
∴f(x)min=f(k)=1+lnk+1=2+lnk,
则2+lnk>k,即2+lnk-k>0,
令g(k)=2+lnk-k,k∈(1,+∞),
g′(k)=
-1<0,
∴g(k)在(1,+∞)上递减,且g(3)=ln3-1>0,g(4)=ln4-2<0,
∴?x0∈(3,4),使g(x0)=0,
故由g(k)>0,可得1<k<x0;
综上,k<x0,
故要使f(x)>k在x∈(1,+∞)时恒成立,最大整数k=3.
f′(x)=
| 1 |
| x |
| k |
| x2 |
| x-k |
| x2 |
①当k≤0时,f′(x)>0,f(x)递增;
②当k>0时,由f′(x)>0,得x>k,由f′(x)<0,得0<x<k;
综上,当k≤0时,f(x)的单调递增区间为(0,+∞);当k>0时,f(x)的单调递减区间为(0,k),单调递增区间为(k,+∞).
(Ⅱ)f(x)>k,
①当k≤1时,由(Ⅰ)知f(x)在(1,+∞)上单调递增,
∴f(x)>f(1)=1+k,则1+k≥k恒成立,
∴此时k≤1;
②当k>1时,由(I)知,f(x)在(1,k)上递减,在(k,+∞)上递增,
∴f(x)min=f(k)=1+lnk+1=2+lnk,
则2+lnk>k,即2+lnk-k>0,
令g(k)=2+lnk-k,k∈(1,+∞),
g′(k)=
| 1 |
| k |
∴g(k)在(1,+∞)上递减,且g(3)=ln3-1>0,g(4)=ln4-2<0,
∴?x0∈(3,4),使g(x0)=0,
故由g(k)>0,可得1<k<x0;
综上,k<x0,
故要使f(x)>k在x∈(1,+∞)时恒成立,最大整数k=3.
点评:该题以函数为载体,考查利用导数研究函数的单调性、最值,考查恒成立问题,考查转化思想,求单调区间注意定义域;解决(Ⅱ)问的关键是恰当构造函数,借助导数研究.

练习册系列答案
相关题目
已知集合A={y|y=3x,x>0},B={x|y=ln(2x-x2)}.则A∩B=( )
| A、(1,2) |
| B、(1,+∞) |
| C、[2,+∞) |
| D、[1,+∞) |
 已知a为如图所示的程序框图输出的结果,则二项式(a
已知a为如图所示的程序框图输出的结果,则二项式(a| x |
| 1 | ||
|
| A、-20 | ||
B、
| ||
| C、-192 | ||
| D、-160 |
已知函数f(x)=3sin(2x-
),则下列结论正确的是( )
| π |
| 4 |
| A、若f(x1)=f(x2)=0,则x1-x2=kπ(k∈Z) | ||||
B、函数f(x)的图象与g(x)=3cos(2x+
| ||||
C、函数f(x)的图象关于(-
| ||||
D、函数f(x)在区间[-
|
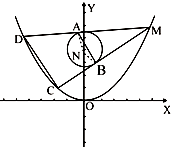 设抛物线E:x2=2y,圆N:x2+(y-4)2=1
设抛物线E:x2=2y,圆N:x2+(y-4)2=1