题目内容
8.已知f′(x)为函数f(x)的导函数,且$f(x)=\frac{1}{2}{x^2}-f(0)+f'(1){e^{x-1}}$,若$g(x)=f(x)-\frac{1}{2}{x^2}+x$,则方程$g(\frac{x^2}{a}-x)-x=0$有且仅有一个根时,a的取值范围是( )| A. | [1,+∞) | B. | (-∞,1] | C. | (0,1] | D. | (-∞,0)∪{1} |
分析 求导,令x=1,即可求得f(0),当x=0,代入f(x),即可求得f′(1),求得f(x)的解析式,由题意可知:由函数y1=$\frac{{x}^{2}}{a}$与函数y2=x+lnx图象可得,方程有且只有一个根时,则a的取值范围是a<0或a=1.
解答 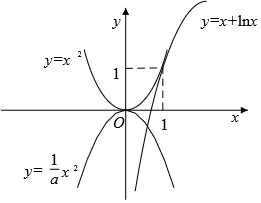 解:由$f(x)=\frac{1}{2}{x^2}-f(0)+f'(1){e^{x-1}}$,求导f′(x)=x-f(0)+f′(1)ex-1,
解:由$f(x)=\frac{1}{2}{x^2}-f(0)+f'(1){e^{x-1}}$,求导f′(x)=x-f(0)+f′(1)ex-1,
故f′(1)=x-f(0)+f′(1),则f(0)=1,
由f(0)=f′(1)e-1=1,则f′(1)=e,
故f(x)=$\frac{1}{2}$x2-x+ex,f′(x)=x-1+ex,
∴g(x)=$\frac{1}{2}$x2-x+ex-$\frac{1}{2}$x2+x=ex,故方程$g(\frac{x^2}{a}-x)-x=0$,${e}^{\frac{{x}^{2}}{a}-x}$=x,
两边取对数可得$\frac{{x}^{2}}{a}$=x+lnx,由函数y1=$\frac{{x}^{2}}{a}$与函数y2=x+lnx图象可得,方程有且只有一个根时,则a的取值范围是a<0或a=1,
当a>1a时无交点,0<a<1时有两个交点.
故a的取值范围(-∞,0)∪{1},
故选D.
点评 本题考查导数的综合应用,考查函数根的个数的判断,考查数形结合思想,属于中档题.

练习册系列答案
相关题目
12.等比数列{an}的各项均为正数,且a1+2a2=4,a42=4a3a7,则a5=( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{16}$ | C. | 20 | D. | 40 |
3.若函数f(x)为奇函数,且在(0,+∞)上是增函数,又f(-3)=0,则不等式x[f(-x)-f(x)]<0的解集为( )
| A. | (-∞,-3)∪(0,3) | B. | (-2,0)∪(3,+∞) | C. | (-3,3) | D. | (-∞,-3)∪(3,+∞) |
20.已知函数f(x)=$\frac{lnx}{x}$,关于x的不等式f2(x)+af(x)>0只有一个整数解,则实数a的取值范围是( )
| A. | (-$\frac{ln3}{3}$,-$\frac{ln2}{2}$] | B. | (-$\frac{1}{e}$,-$\frac{ln2}{2}$] | C. | [$\frac{ln2}{2}$,-$\frac{ln3}{3}$] | D. | [$\frac{ln2}{2}$,$\frac{1}{e}$) |