题目内容
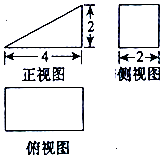
14.某几何体的三视图如图所示,则该几何体的体积为( )
| A. | 2 | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
分析 如图所示,该几何体为三棱锥P-ABC,AB⊥BC.过点P作PO⊥底面ABC,垂足为O.AO$\underset{∥}{=}$BC.
解答 解:如图所示,该几何体为三棱锥P-ABC,AB⊥BC.过点P作PO⊥底面ABC,垂足为O.AO$\underset{∥}{=}$BC.
∴该几何体的体积V=$\frac{1}{3}×\frac{1}{2}×1×1$×1=$\frac{1}{6}$.
故选:D.
点评 本题考查了三棱锥的三视图、体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.某几何体的三视图如图所示,则该几何体的表面积是( )

| A. | $20+4\sqrt{5}$ | B. | $12+4\sqrt{5}$ | C. | $20+2\sqrt{5}$ | D. | $12+2\sqrt{5}$ |
3.若函数f(x)为奇函数,且在(0,+∞)上是增函数,又f(-3)=0,则不等式x[f(-x)-f(x)]<0的解集为( )
| A. | (-∞,-3)∪(0,3) | B. | (-2,0)∪(3,+∞) | C. | (-3,3) | D. | (-∞,-3)∪(3,+∞) |
7.为了解某社区居民购买水果和牛奶的年支出费用与购买食品的年支出费用的关系,随机调查了该社区5户家庭,得到如下统计数据表:
根据上表可得回归直线方程$\hat y=\hat bx+\hat a$,其中$\hat b=0.85,\hat a=\overline y-\hat b\overline x$,据此估计,该社区一户购买食品的年支出费用为3.00万元的家庭购买水果和牛奶的年支出费用约为( )
| 购买食品的年支出费用x(万元) | 2.09 | 2.15 | 2.50 | 2.84 | 2.92 |
| 购买水果和牛奶的年支出费用y(万元) | 1.25 | 1.30 | 1.50 | 1.70 | 1.75 |
| A. | 1.79万元 | B. | 2.55万元 | C. | 1.91万元 | D. | 1.94万元 |
8.双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}$=1(a>0,b>0)的离心率为$\sqrt{10}$,则其渐近线方程为( )
| A. | y=±3x | B. | $y=±\frac{1}{2}x$ | C. | y=±2x | D. | $y=±\frac{1}{3}x$ |
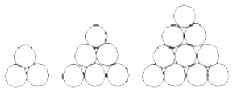 在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第一堆只有一层,就一个乒乓球;第2、3、4、…堆最底层(第一层)分别按图所示方式固定摆放.从第一层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以f(n)表示第n堆的乒乓球总数,则f(3)=10;f(n)=$\frac{1}{6}$n(n+1)(n+2)(答案用n表示).
在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第一堆只有一层,就一个乒乓球;第2、3、4、…堆最底层(第一层)分别按图所示方式固定摆放.从第一层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以f(n)表示第n堆的乒乓球总数,则f(3)=10;f(n)=$\frac{1}{6}$n(n+1)(n+2)(答案用n表示).