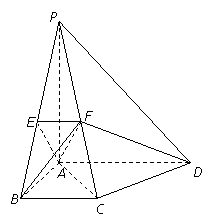
题目内容
如图,在四棱锥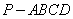 中,平面
中,平面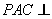 平面
平面 ,且
,且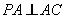 ,
, 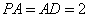 .四边形
.四边形 满足
满足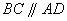 ,
,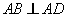 ,
,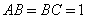 .点
.点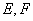 分别为侧棱
分别为侧棱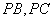 上的点,且
上的点,且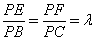 .
.
(Ⅰ)求证: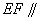 平面
平面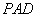 ;
;
(Ⅱ)当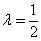 时,求异面直线
时,求异面直线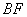 与
与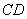 所成角的余弦值;
所成角的余弦值;
(Ⅲ)是否存在实数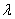 ,使得平面
,使得平面 平面
平面 ?若存在,试求出
?若存在,试求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 |
证明:(Ⅰ)由已知, ,
,
所以  .
.
因为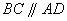 ,所以
,所以 .
.
而 平面
平面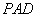 ,
, 平面
平面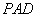 ,
,
所以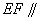 平面
平面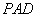 .
.
(Ⅱ)因为平面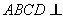 平面
平面 ,
,
平面 平面
平面 ,且
,且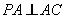 ,
,
所以 平面
平面 .
.
所以 ,
, .
.
又因为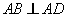 ,
,
所以 两两垂直. …
两两垂直. …
如图所示,建立空间直角坐标系,
因为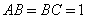 ,
,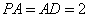 ,
,
所以
 .
.
当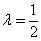 时,
时, 为
为 中点,
中点,
所以 ,
,
所以 .
.
设异面直线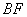 与
与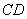 所成的角为
所成的角为 ,
,
所以 ,
,
所以异面直线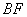 与
与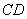 所成角的余弦值为
所成角的余弦值为 .
.
(Ⅲ)设 ,则
,则 .
.
由已知 ,所以
,所以 ,
,
所以 所以
所以 .
.
设平面 的一个法向量为
的一个法向量为 ,因为
,因为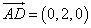 ,
,
所以 即
即
令 ,得
,得 .
.
设平面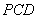 的一个法向量为
的一个法向量为 ,因为
,因为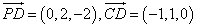 ,
,
所以 即
即
令 ,则
,则 .
.
若平面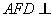 平面
平面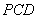 ,则
,则 ,所以
,所以 ,解得
,解得 .
.
所以当 时,平面
时,平面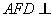 平面
平面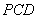 .…
.…

练习册系列答案
相关题目
 ,其中
,其中 表示不超过实数
表示不超过实数 的最大整数,如
的最大整数,如 .若
.若 ,则
,则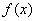 的值域为 .
的值域为 .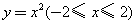 绕
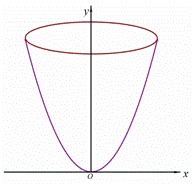
绕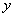 轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的体积是
轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的体积是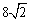 (D)
(D)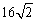
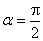 ”是“
”是“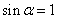 ”的充要条件;
”的充要条件; 的展开式中的常数项为
的展开式中的常数项为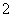 ;
;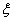 ~
~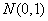 ,若
,若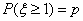 ,则
,则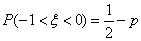 .
. 是
是 的外接圆,过点C作圆
的外接圆,过点C作圆 的切线交
的切线交 的延长线于点
的延长线于点 .若
.若 ,
, ,则线段
,则线段 的长是 ;圆
的长是 ;圆
 ,
, ,则
,则
 B.
B.  C.
C.  D.
D. 
 的右焦点为焦点,顶点在原点的抛物线的标准方程是 .
的右焦点为焦点,顶点在原点的抛物线的标准方程是 .  ”是“关于
”是“关于 的不等式组
的不等式组 表示的平面区域为三角形”的
表示的平面区域为三角形”的 必要条件
必要条件  B. 必要不充分条件
B. 必要不充分条件  的非空子集,且当
的非空子集,且当 时,有
时,有 .记满足条件的集合M的个数为
.记满足条件的集合M的个数为 ,则
,则 ;
; 。
。