题目内容
甲和乙等五名志愿者被随机地分到A、B、C、D四个不同的岗位服务,每个岗位至少有一名志愿者,则甲和乙在不同岗位服务的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:所有的结果共有C52A44种,不满足条件的事件数A44 ,可得不满足条件的概率,用1减去此概率即得所求.
解答:
解:5个人分到4个岗位,每个岗位至少有一名志愿者共有C52A44=240种结果,
甲和乙在同一岗位服务的事件数A44 =24
则甲和乙不在同一岗位服务的概率为 1-
=
故选:A
甲和乙在同一岗位服务的事件数A44 =24
则甲和乙不在同一岗位服务的概率为 1-
| 24 |
| 240 |
| 9 |
| 10 |
故选:A
点评:本题主要考查古典概型和排列组合,排列与组合问题要区分开,若题目要求元素的顺序则是排列问题,排列问题要做到不重不漏,有些题目带有一定的约束条件,解题时要先考虑有限制条件的元素,属于中档题.

练习册系列答案
相关题目
半径为R的球内接一个正方体,则该正方体的体积是( )
A、2
| ||||
B、
| ||||
C、
| ||||
D、
|
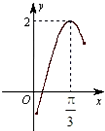
函数f(x)=Asin(2x+Φ)(A>0,Φ∈R)的部分图象如图所示,则f(-
)=( )
| π |
| 24 |

| A、-1 | ||||
B、-
| ||||
C、-
| ||||
D、-
|