题目内容
某分公司经销某种品牌产品,每件产品的成本为4元,并且每件产品需向总公司交a元(3≤a≤6)的管理费,预计当每件产品的售价为x元(11≤x≤14)时,一年的销售量为(16-x)2万件.
(1)求分公司一年的利润L(万元)与每件产品的售价x的函数关系式;
(2)求分公司一年的利润的最大值Q(a).
(1)求分公司一年的利润L(万元)与每件产品的售价x的函数关系式;
(2)求分公司一年的利润的最大值Q(a).
考点:函数模型的选择与应用
专题:应用题,导数的综合应用
分析:(1)求出每件产品的利润,乘以价格得到利润L(万元)与每件产品的售价x的函数关系式;
(2)求出利润函数的导函数,由a得范围得到导函数零点的范围,分类讨论原函数在[11,14]上的单调性,并求出a在不同范围内的利润函数的最值.
(2)求出利润函数的导函数,由a得范围得到导函数零点的范围,分类讨论原函数在[11,14]上的单调性,并求出a在不同范围内的利润函数的最值.
解答:
解:(1)每件产品的利润为:x-4-a元,
分公司一年的利润L(万元)与售价x的函数关系式为:L=(x-4-a)(16-x)2,x∈[11,14];
(2)L′(x)=(16-x)2-2(x-4-a)(16-x)
=(16-x)(-3x+24+2a).
令L′(x)=0,得x=8+
a或x=16(不合题意,舍去).
∵3≤a≤6,∴10≤8+
a≤12.
在x=8+
a左右两侧,L′(x)的值由正变负.
∴当10≤8+
a≤11,最大值Q(a)=L(11)=25(7-a);
当11≤8+
a≤12,最大值Q(a)=L(8+
a)=36(6-a)=4(4-
)3.
分公司一年的利润L(万元)与售价x的函数关系式为:L=(x-4-a)(16-x)2,x∈[11,14];
(2)L′(x)=(16-x)2-2(x-4-a)(16-x)
=(16-x)(-3x+24+2a).
令L′(x)=0,得x=8+
| 2 |
| 3 |
∵3≤a≤6,∴10≤8+
| 2 |
| 3 |
在x=8+
| 2 |
| 3 |
∴当10≤8+
| 2 |
| 3 |
当11≤8+
| 2 |
| 3 |
| 2 |
| 3 |
| a |
| 3 |
点评:本题考查函数、导数及其应用等知识,考查运用数学知识分析和解决实际问题的能力,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数f(x)=Asin(2x+Φ)(A>0,Φ∈R)的部分图象如图所示,则f(-
)=( )
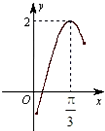
| π |
| 24 |

| A、-1 | ||||
B、-
| ||||
C、-
| ||||
D、-
|
