题目内容
求适合下列条件的直线方程:
(1)经过点P(3,2)且在两坐标轴上的截距相等;
(2)经过点A(-1,-3),倾斜角等于直线y=3x的倾斜角的2倍.
(1)经过点P(3,2)且在两坐标轴上的截距相等;
(2)经过点A(-1,-3),倾斜角等于直线y=3x的倾斜角的2倍.
考点:待定系数法求直线方程
专题:计算题,直线与圆
分析:(1)当横截距a=0时,纵截距b=0,此时直线过点(0,0),P(3,2);当横截距a≠0时,纵截距b=a,此时直线方程设为x+y=a,把P(3,2)代入,解得a=5.由此能求出过点P(3,2)且在两坐标轴上的截距相等的直线方程.
(2)先假设直线y=3x的倾斜角是A,进而根据直线倾斜角与斜率之间的关系得到tanA=3,然后根据正切函数的二倍角公式求出所求直线的斜率,最后根据点斜式方程得到答案.
(2)先假设直线y=3x的倾斜角是A,进而根据直线倾斜角与斜率之间的关系得到tanA=3,然后根据正切函数的二倍角公式求出所求直线的斜率,最后根据点斜式方程得到答案.
解答:
解:(1)当横截距a=0时,纵截距b=0,此时直线过点(0,0),P(3,2),
∴直线方程为y=
x;
当横截距a≠0时,纵截距b=a,此时直线方程设为x+y=a,
把P(3,2)代入,解得a=5,
∴所求的直线方程为:x+y-5=0.
综上:过点P(3,2)且在两坐标轴上的截距相等的直线方程为3x-2y=0或x+y-5=0.
(2)假设y=3x的倾斜角是A,那么有tanA=3
设过A点直线的倾斜角是B,那么B=2A
那么直线L的斜率k=tanB=tan2A=
=-
∴直线方程是:y+3=-
(x+1),即:直线方程为3x+4y+15=0.
∴直线方程为y=
| 3 |
| 2 |
当横截距a≠0时,纵截距b=a,此时直线方程设为x+y=a,
把P(3,2)代入,解得a=5,
∴所求的直线方程为:x+y-5=0.
综上:过点P(3,2)且在两坐标轴上的截距相等的直线方程为3x-2y=0或x+y-5=0.
(2)假设y=3x的倾斜角是A,那么有tanA=3
设过A点直线的倾斜角是B,那么B=2A
那么直线L的斜率k=tanB=tan2A=
| 2×3 |
| 1-32 |
| 3 |
| 4 |
∴直线方程是:y+3=-
| 3 |
| 4 |
点评:本题考查直线方程的求法,考查正切函数的二倍角公式,解题时要注意截距式方程的合理运用.

练习册系列答案
相关题目
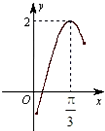
函数f(x)=Asin(2x+Φ)(A>0,Φ∈R)的部分图象如图所示,则f(-
)=( )
| π |
| 24 |

| A、-1 | ||||
B、-
| ||||
C、-
| ||||
D、-
|
用“二分法”求方程x3-2x-1=0的一个近似解时,现在已经将一根锁定在在区间(1,2)内,则下一步可断定该根所在的区间为( )
| A、(1,1.4) |
| B、(1.4,2) |
| C、(1,1.5) |
| D、(1.5,2) |