题目内容
已知AB是⊙O的切线,在下列条件中,能判定AB⊥CD的是( )
| A、AB与⊙O相切于点C,CD为⊙O的一条弦 |
| B、CD过圆心O |
| C、AB与⊙O相切于点C,CD过圆心 |
| D、CD也是⊙O的切线 |
考点:圆的切线的性质定理的证明
专题:直线与圆
分析:利用圆的切线的性质定理对四个命题分别进行判断,能得到正确结果.
解答:
解:∵AB是⊙O的切线,AB与⊙O相切于点C,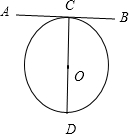
CD为⊙O的一条弦,
∴当且仅当CD过圆心时,AB⊥CD,
∴当CD不过圆心时,不能判定AB⊥CD,故A不正确;
∵AB是⊙O的切线,CD过圆心O,
∴当且仅当CD过AB与圆的切点时,AB⊥CD,
∴当CD不过AB与圆的切点时,不能判定AB⊥CD,故B不正确;
∵AB是⊙O的切线,AB与⊙O相切于点C,CD过圆心,
∴由圆的切线的性质定理得到AB⊥CD,故C正确;
∵AB是⊙O的切线,CD也是⊙O的切线,
∴AB与CD相交或平行,不能判定AB⊥CD,故D不正确.
故选:C.

CD为⊙O的一条弦,
∴当且仅当CD过圆心时,AB⊥CD,
∴当CD不过圆心时,不能判定AB⊥CD,故A不正确;
∵AB是⊙O的切线,CD过圆心O,
∴当且仅当CD过AB与圆的切点时,AB⊥CD,
∴当CD不过AB与圆的切点时,不能判定AB⊥CD,故B不正确;
∵AB是⊙O的切线,AB与⊙O相切于点C,CD过圆心,
∴由圆的切线的性质定理得到AB⊥CD,故C正确;
∵AB是⊙O的切线,CD也是⊙O的切线,
∴AB与CD相交或平行,不能判定AB⊥CD,故D不正确.
故选:C.
点评:本题考查圆的切线的性质定理的应用,是基础题,解题时要熟练掌握圆的切线的性质定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
二进制数101110(2)转化为八进制数为( )
| A、45(8) |
| B、56(8) |
| C、67(8) |
| D、78(8) |
判断下列命题的真假,其中为真命题的是( )
| A、?x∈R,x2+1=0 |
| B、?x∈R,x2+1=0 |
| C、?x∈R,sinx<tanx |
| D、?x∈R,sinx<tanx |
一名同学想要报考某大学,他必须从该校的7个不同的专业中选出5个,并按第一志愿,第二志愿,…,第五志愿顺序填进志愿表,若A专业不能作为第一志愿,B专业不能作为第二志愿,且A、B专业不能相邻,则不同的填法种数有( )
| A、1560 | B、1500 |
| C、1080 | D、960 |
已知i为虚数单位,则复数
在复平面上所对应的点在( )
| 2-i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
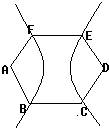 如图,正六边形ABCDEF的两个顶点A、D为双曲线的焦点,其余四个顶点都在双曲线上,则该双曲线的离心率为
如图,正六边形ABCDEF的两个顶点A、D为双曲线的焦点,其余四个顶点都在双曲线上,则该双曲线的离心率为