题目内容
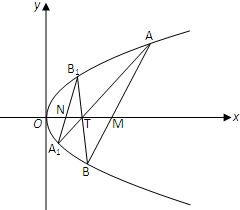已知直线l：y=2x-4与抛物线C：y2=4x相交于A，B两点，T（t，0）（t＞0且t≠2）为x轴上任意一点，连接AT，BT并延长与抛物线C分别相交于A1，B1．（1）设A1B1斜率为k，求证：k•t为定值；
（2）设直线AB，A1B1与x轴分别交于M，N，令S△ATM=S1，S△BTM=S2，S△B1TN=S3，S△A1TN=S4，若S1，S2，S3，S4构成等比数列，求t的值．
考点：抛物线的简单性质,等比关系的确定
专题：圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析：（1）由已知条件推导出A（4，4），B（1，-2），设A1(
，m)，B1(
，n)，由kAT=kA1T，求出A1（
，-t），B1(t2，2t)，由此能证明k•t=4是定值．
（2）直线A1B1：y-2t=
(x-t2)，令y=0，得N（
，0），由M（2，0），推导出S2=
S1，S4=
S1，S3=
S1，由S1，S2，S3，S4构成等比数列，能求出t的值．
| m2 |
| 4 |
| n2 |
| 4 |
| t2 |
| 4 |
（2）直线A1B1：y-2t=
| 4 |
| t |
| t2 |
| 2 |
| 1 |
| 2 |
| t2 |
| 8 |
| t2 |
| 4 |
解答：
解：（1）解方程组
，得
，或
，
∴A（4，4），B（1，-2），
设A1(
，m)，B1(
，n)，
∵T（t，0）（t＞0且t≠2）为x轴上任意一点，
连接AT，BT并延长与抛物线C分别相交于A1，B1，
∴kAT=kA1T，即
=
，
∴m2-4t=4m-tm，
∴m（m-4）=t（4-m），
m=4时，易得k•t=4是定值，
m≠4时，有m=-t，∴A1（
，-t），
同理：B1(t2，2t)，
∴k=
=
，
∴k•t=4是定值．（5分）
（2）∵A1（
，-t），B1(t2，2t)，
∴直线A1B1：
=
，
即y-2t=
(x-t2)，令y=0，得N（
，0），
∵M（2，0），∴
=|
|=2，
∴S2=
S1，
=|
|=|
•
|=
，
∴S4=
S1，
=|
|=|
•
|=
，
∴S3=
S1，
∵S1，S2，S3，S4构成等比数列，
∴t2=1，
∵t＞0，∴t=1，
∴t的值是1．（10分）
|
|
|
∴A（4，4），B（1，-2），
设A1(
| m2 |
| 4 |
| n2 |
| 4 |
∵T（t，0）（t＞0且t≠2）为x轴上任意一点，
连接AT，BT并延长与抛物线C分别相交于A1，B1，
∴kAT=kA1T，即
| 4 |
| 4-t |
| m | ||
|
∴m2-4t=4m-tm，
∴m（m-4）=t（4-m），
m=4时，易得k•t=4是定值，
m≠4时，有m=-t，∴A1（
| t2 |
| 4 |
同理：B1(t2，2t)，
∴k=
| 3t | ||
t2-
|
| 4 |
| t |
∴k•t=4是定值．（5分）
（2）∵A1（
| t2 |
| 4 |
∴直线A1B1：
| y-2t |
| x-t2 |
| -t-2t | ||
|
即y-2t=
| 4 |
| t |
| t2 |
| 2 |
∵M（2，0），∴
| S1 |
| S2 |
| yA |
| yB |
∴S2=
| 1 |
| 2 |
| S4 |
| S1 |
| TM•yA1 |
| TE•yA |
| ||
| t-2 |
| t |
| 4 |
| t2 |
| 8 |
∴S4=
| t2 |
| 8 |
| S3 |
| S1 |
| TN•yB1 |
| TM•yA |
| ||
| t-2 |
| 2t |
| 4 |
| t2 |
| 4 |
∴S3=
| t2 |
| 4 |
∵S1，S2，S3，S4构成等比数列，
∴t2=1，
∵t＞0，∴t=1，
∴t的值是1．（10分）
点评：本题考查抛物线与直线的位置关系及其应用，涉及到等比数列、直线方程、抛物线等知识点，综合性强，难度大，解题时要注意等价转化思想的合理运用．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
判断下列命题的真假，其中为真命题的是（ ）
| A、?x∈R，x2+1=0 |
| B、?x∈R，x2+1=0 |
| C、?x∈R，sinx＜tanx |
| D、?x∈R，sinx＜tanx |