题目内容
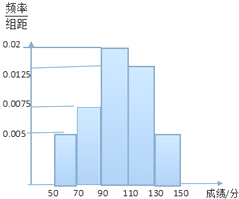 某班学生参加科普知识竞赛,成绩的频率分布直方图如图,数据的分布组依次为[50,70),[70,90),[90,110),[110,130),[130,150),已知成绩低于90分的学生人数为10人.
某班学生参加科普知识竞赛,成绩的频率分布直方图如图,数据的分布组依次为[50,70),[70,90),[90,110),[110,130),[130,150),已知成绩低于90分的学生人数为10人.(1)求成绩不低于130分的学生人数n;
(2)成绩不低于130分的这n名学生,继续选择甲、乙两组题目进行表演赛,约定:每人通过掷一枚质地均匀的骰子决定自己去选择哪组题目,掷出点数位1或2的人选择甲组,掷出点大于2的人选择乙组题目.
(Ⅰ)求这n名同学中恰有2人选择甲组题目的概率;
(Ⅱ)用X,Y分别表示这n名同学中选择甲、乙组题目的人数,记ξ=|X-Y|,求随机变量的分布列与数学期望Eξ.
考点:离散型随机变量的期望与方差,频率分布直方图,古典概型及其概率计算公式
专题:综合题,概率与统计
分析:(1)求出绩低于90分的学生的频率,利用成绩低于90分的学生人数为10人,可得参加科普知识竞赛的人数,求出成绩不低于130分的频率,即可得出结论;
(2)(Ⅰ)求出每个人去参加甲游戏的概率,去参加乙游戏的人数的概率.设“这4个人中恰有i人去参加甲游戏”为事件Ai(i=0,1,2,3,4),故P(A2)=
(
)2(
)2,由此能求出这4个人中恰有2人去参加甲游戏的概率.
(Ⅱ)ξ的所有可能取值为0,2,4,由于A1与A3互斥,A0与A4互斥,求出相应的概率,可得ξ的分布列与数学期望.
(2)(Ⅰ)求出每个人去参加甲游戏的概率,去参加乙游戏的人数的概率.设“这4个人中恰有i人去参加甲游戏”为事件Ai(i=0,1,2,3,4),故P(A2)=
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
(Ⅱ)ξ的所有可能取值为0,2,4,由于A1与A3互斥,A0与A4互斥,求出相应的概率,可得ξ的分布列与数学期望.
解答:
解:(1)成绩低于90分的学生的频率为(0.0075+0.005)×20=0.25,
∵成绩低于90分的学生人数为10人,
∴参加科普知识竞赛共有
=40人,
成绩不低于130分的频率为1-(0.02+0.0125+0.0075+0.005)×20=0.1,
∴成绩不低于130分的学生人数n=0.1×40=4人;
(2)(Ⅰ)依题意,这4个人中,每个人去参加甲游戏的概率为
,去参加乙游戏的人数的概率为
.
设“这4个人中恰有2人去参加甲游戏”为事件Ai(i=0,1,2,3,4),
∴这4个人中恰有2人去参加甲游戏的概率为P(A2)=
(
)2(
)2=
.
(Ⅱ)ξ的所有可能取值为0,2,4,由于A1与A3互斥,A0与A4互斥,
故P(ξ=0)=P(A2)=
,
P(ξ=2)=P(A1)+P(A3)=
,
P(ξ=4)=P(A0)+P(A4)=
,
∴ξ的分布列是
数学期望Eξ=0×
+2×
+4×
=
.
∵成绩低于90分的学生人数为10人,
∴参加科普知识竞赛共有
| 10 |
| 0.25 |
成绩不低于130分的频率为1-(0.02+0.0125+0.0075+0.005)×20=0.1,
∴成绩不低于130分的学生人数n=0.1×40=4人;
(2)(Ⅰ)依题意,这4个人中,每个人去参加甲游戏的概率为
| 1 |
| 3 |
| 2 |
| 3 |
设“这4个人中恰有2人去参加甲游戏”为事件Ai(i=0,1,2,3,4),
∴这4个人中恰有2人去参加甲游戏的概率为P(A2)=
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 27 |
(Ⅱ)ξ的所有可能取值为0,2,4,由于A1与A3互斥,A0与A4互斥,
故P(ξ=0)=P(A2)=
| 8 |
| 27 |
P(ξ=2)=P(A1)+P(A3)=
| 40 |
| 81 |
P(ξ=4)=P(A0)+P(A4)=
| 17 |
| 81 |
∴ξ的分布列是
| ξ | 0 | 2 | 4 | ||||||
| P |
|
|
|
| 8 |
| 27 |
| 40 |
| 81 |
| 17 |
| 81 |
| 148 |
| 81 |
点评:本题考查概率知识的求解,考查频率分布直方图,考查互斥事件的概率公式,考查离散型随机变量的分布列与期望,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
判断下列命题的真假,其中为真命题的是( )
| A、?x∈R,x2+1=0 |
| B、?x∈R,x2+1=0 |
| C、?x∈R,sinx<tanx |
| D、?x∈R,sinx<tanx |
已知i为虚数单位,则复数
在复平面上所对应的点在( )
| 2-i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
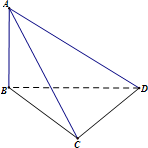 如图,在四面体ABCD中,AB⊥平面BCD,△BCD是边长为
如图,在四面体ABCD中,AB⊥平面BCD,△BCD是边长为