题目内容
已知点P(1,1)是直线l被椭圆
+
=1所截得的弦的中点,则直线l的方程为 .
| x2 |
| 2 |
| y2 |
| 4 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设A(x1,y1),B(x2,y2),利用点差法能够求出直线l的方程.
解答:
解:设A(x1,y1),B(x2,y2),则
2x12+y12=4,2x22+y22=4,
两式相减可得:2(x1+x2)(x1-x2)+(y1+y2)(y1-y2)=0,
∴4(x1-x2)+2(y1-y2)=0,
∴kl=-
,
∴直线l的方程为y-1=-
(x-1),即2x+y-3=0.
故答案为:2x+y-3=0.
2x12+y12=4,2x22+y22=4,
两式相减可得:2(x1+x2)(x1-x2)+(y1+y2)(y1-y2)=0,
∴4(x1-x2)+2(y1-y2)=0,
∴kl=-
| 1 |
| 2 |
∴直线l的方程为y-1=-
| 1 |
| 2 |
故答案为:2x+y-3=0.
点评:本题考查直线方程的求法,解题时要认真审题,仔细解答,注意点差法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
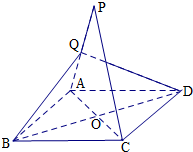 如图,P是菱形ABCD所在平面外一点,Q是PA中点,且QB=QD.
如图,P是菱形ABCD所在平面外一点,Q是PA中点,且QB=QD.