题目内容
平面向量
=(3,-4),
=(2,x),
=(2,y),已知
∥
,
⊥
.
(1)求
•
及
与
夹角;
(2)求
在
上的投影;
(3)求|
+
|的值.
| a |
| b |
| c |
| a |
| b |
| a |
| c |
(1)求
| b |
| c |
| b |
| c |
(2)求
| b |
| c |
(3)求|
| a |
| c |
考点:数量积表示两个向量的夹角,向量的模,平面向量数量积的运算
专题:平面向量及应用
分析:(1)由平行和垂直关系分别可得x和y的值,可得向量的坐标,易得
•
=0,
与
夹角为90°;
(2)由(1)
与
夹角为90°,易得
在
上的投影为0;
(3)由(1)可得
+
=(5,-
),由模长公式可得.
| b |
| c |
| b |
| c |
(2)由(1)
| b |
| c |
| b |
| c |
(3)由(1)可得
| a |
| c |
| 5 |
| 2 |
解答:
解:(1)∵
=(3,-4),
=(2,x),
=(2,y),
由
∥
可得3x-(-4)×2=0,解得x=-
,
由
⊥
可得3×2-4y=0,解得y=
,
∴
=(2,-
),
=(2,
),
∴
•
=2×2-
×
=0,
∴
与
夹角为90°;
(2)由(1)
与
夹角为90°
∴
在
上的投影为0;
(3)由(1)
+
=(5,-
),
∴|
+
|=
=
| a |
| b |
| c |
由
| a |
| b |
| 8 |
| 3 |
由
| a |
| c |
| 3 |
| 2 |
∴
| b |
| 8 |
| 3 |
| c |
| 3 |
| 2 |
∴
| b |
| c |
| 8 |
| 3 |
| 3 |
| 2 |
∴
| b |
| c |
(2)由(1)
| b |
| c |
∴
| b |
| c |
(3)由(1)
| a |
| c |
| 5 |
| 2 |
∴|
| a |
| c |
52+(-
|
5
| ||
| 2 |
点评:本题考查平面向量的数量积和平行垂直关系,涉及投影和模长公式,属基础题.

练习册系列答案
相关题目
两人同时向一敌机射击,甲的命中率为
,乙的命中率为
,则两人中恰有一人击中敌机的概率为( )
| 1 |
| 5 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知Sn是等差数列{an}的前n项和,若a3=4,则S5=( )
| A、5 | B、10 | C、15 | D、20 |
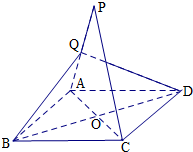 如图,P是菱形ABCD所在平面外一点,Q是PA中点,且QB=QD.
如图,P是菱形ABCD所在平面外一点,Q是PA中点,且QB=QD.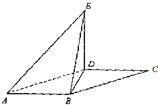 如图,平行四边形ABCD中,BD⊥AB,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD,证明:AB⊥面BDE.
如图,平行四边形ABCD中,BD⊥AB,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD,证明:AB⊥面BDE.