题目内容
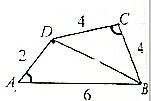已知在四边形ABCD中，∠BAD+∠BCD=π，AB=6，BC=CD=4，AD=2，求BD的长．考点：解三角形
专题：计算题,解三角形
分析：在△ABD中和△BCD中，运用余弦定理，再由∠BAD+∠BCD=π，则cos∠BAD+cos∠BCD=0，计算即可得到BD．
解答：
解：在△ABD中，cos∠BAD=
=
=
，
在△BCD中，cos∠BCD=
=
=
．
由∠BAD+∠BCD=π，
则cos∠BAD+cos∠BCD=0，
即有
+
=0，
即BD2=
，
解得BD=
．
| AD2+AB2-BD2 |
| 2AD•AB |
=
| 4+36-BD2 |
| 2×2×6 |
| 40-BD2 |
| 24 |
在△BCD中，cos∠BCD=
| BC2+CD2-BD2 |
| 2BC•CD |
=
| 16+16-BD2 |
| 2×4×4 |
| 32-BD2 |
| 32 |
由∠BAD+∠BCD=π，
则cos∠BAD+cos∠BCD=0，
即有
| 40-BD2 |
| 24 |
| 32-BD2 |
| 32 |
即BD2=
| 256 |
| 7 |
解得BD=
16
| ||
| 7 |
点评：本题考查余弦定理及运用，同时考查诱导公式的运用，考查运算能力，属于基础题．
练习册系列答案
相关题目
已知α∈（-π，0），sin（α+
）=
，则tan（2α+
）=（ ）
| π |
| 2 |
| 4 |
| 5 |
| π |
| 4 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60°，PA=PD=AD=2，点M在线段PC上，且PM=2MC，N为AD的中点