题目内容
抛物线x2=ky与曲线y=lnx的公共切线方程为 .
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:联立两曲线方程,消去y,分离参数k=
,设f(x)=
,求出导数,得到单调区间和极值,这也是两函数图象相切的临界值,进而得到切点,由(lnx)′=
,即有切线斜率,再由点斜式方程,即可得到所求切线方程.
| x2 |
| lnx |
| x2 |
| lnx |
| 1 |
| x |
解答:
解:抛物线为y=
•x2,曲线为y=lnx,其中x>0,
联立方程得,
•x2=lnx,分离参数k=
设f(x)=
,则f'(x)=
,
由f′(x)=0,解得x=
,
由于x>
时,f(x)递增,0<x<
递减,
则f(x)在x=
处取得极小值,这也是两函数图象相切的临界值,
此时参数k=f(
)=2e(这个k不是斜率),切点为(
,
),
由于(lnx)′=
,即有切线斜率为
,
公切线的方程为:y-
=
(x-
),即为
y=
x-
.
故答案为:y=
x-
.
| 1 |
| k |
联立方程得,
| 1 |
| k |
| x2 |
| lnx |
设f(x)=
| x2 |
| lnx |
| x(2lnx-1) |
| (lnx)2 |
由f′(x)=0,解得x=
| e |
由于x>
| e |
| e |
则f(x)在x=
| e |
此时参数k=f(
| e |
| e |
| 1 |
| 2 |
由于(lnx)′=
| 1 |
| x |
| 1 | ||
|
公切线的方程为:y-
| 1 |
| 2 |
| 1 | ||
|
| e |
y=
| 1 | ||
|
| 1 |
| 2 |
故答案为:y=
| 1 | ||
|
| 1 |
| 2 |
点评:本题考查导数的运用:求切线方程,联立方程运用导数求得极值点,得到切点是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图是一个算法的程序框图,最后输出的W是( )


| A、22 | B、23 | C、24 | D、25 |
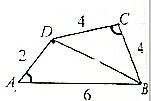 已知在四边形ABCD中,∠BAD+∠BCD=π,AB=6,BC=CD=4,AD=2,求BD的长.
已知在四边形ABCD中,∠BAD+∠BCD=π,AB=6,BC=CD=4,AD=2,求BD的长.