Question

在三棱锥P-ABC中，PA⊥平面ABC，AB⊥BC，AB=BC=

2

，PA=2，则此三棱锥外接球的体积为

 

．

Answer 1

考点：球的体积和表面积,棱锥的结构特征

专题：综合题,空间位置关系与距离

分析：解题思路：“找球心”（到三棱锥四个顶点距离相等等的点）．注意到PC是Rt△PAC和Rt△PBC的公共的斜边，记它的中点为O，从而得出该三棱锥的外接球球心为O，半径为

2

，从而计算出它的体积即可．

解答： 解：∵PC是Rt△PAC和Rt△PBC的公共的斜边，
记它的中点为O，则OA=OB=OP=OC=

1

2

PC=

2

，即该三棱锥
的外接球球心为O，半径为

2

，
故它的体积为：

4

3

π•(

2

)3=

8 2

3

π．
故答案为：

8 2

3

π

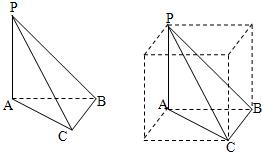
点评：本题主要考查线线垂直、线面平行、求球的体积等立体几何知识，以及分析问题与解决问题的能力．本题还有方法二：“补体”，将三棱锥补成长方体，如图所示；它的对角线PC是其外接球的直径，从而即可求得球的体积．