题目内容
在（1-x）（1+x）3的展开式中，x3的系数是（ ）
| A、2 | B、-2 | C、1 | D、-1 |
考点：二项式系数的性质
专题：计算题,二项式定理
分析：结合二项式定理，化简表达式为（1-x2）（1+x）2，然后求出展开式中x3的系数即可．
解答：
解：（1-x）（1+x）3=（1-x2）（1+x）2，
（1+x）（1-x）3展开式中x3的系数，只需求解（1+x）2中的x的系数与（1-x2）中x2项的系数的乘积，
∴（1+x）（1-x）3展开式中x3的系数是：-1×2=-2．
故选：B．
（1+x）（1-x）3展开式中x3的系数，只需求解（1+x）2中的x的系数与（1-x2）中x2项的系数的乘积，
∴（1+x）（1-x）3展开式中x3的系数是：-1×2=-2．
故选：B．
点评：本题考查二项式定理的应用，二项式定理系数的性质，特定项的求法，考查计算能力．
练习册系列答案
相关题目
已知y=f（x）+x2是奇函数，且f（1）=1，若g（x）=f（x）-x2，则g（-1）=（ ）
| A、-4 | B、-3 | C、-1 | D、0 |
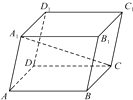如图所示，在平行六面体ABCD-A1B1C1D1中，若| A1B1 |
| a |
| A1D1 |
| b |
| AA1 |
| c |
| A1C |
A、-
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知集合，则A={{1，2，3，4，5，6}，B={y|y=
，x∈A}，则 A∩B=（ ）
| x |
| A、{1，2} |
| B、{1，2，3} |
| C、{1，3，5} |
| D、{1，2，3，4，5，6} |