题目内容
某公园设有甲,乙,丙三关的闯关游戏,且通过甲,乙,丙三关的概率分别为
,
,
,甲,乙,丙三关的过关得分分别记为4分,2分,4分,若某关没有闯过,则该关得分记为0分,各关之间互不影响
(1)若闯关得分不低于8分则获奖,求获奖的概率
(2)记闯关成功的个数为随机变量ξ,求ξ的分布列与数学期望.
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
(1)若闯关得分不低于8分则获奖,求获奖的概率
(2)记闯关成功的个数为随机变量ξ,求ξ的分布列与数学期望.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(1)闯关得分不低于8分包含两种情况通过三关或通过甲、丙两关但乙关没通过,由此能求出获奖的概率.(2)由已知得ξ=0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
解答:
解:(1)闯关得分不低于8分包含两种情况:
通过三关或通过甲、丙两关但乙关没通过,
∴获奖的概率P=
×
×
+
×(1-
)×
=
+
=
.
(2)由已知得ξ=0,1,2,3,
P(ξ=0)=(1-
)(1-
)(1-
)=
,
P(ξ=1)=
(1-
)(1-
)+(1-
)×
×(1-
)+(1-
)(1-
)×
=
,
P(ξ=2)=
×
×(1-
)+
×(1-
)×
+(1-
)×
×
=
,
P(ξ=3)=
×
×
=
,
∴ξ的分布列为:
Eξ=0×
+1×
+2×
+3×
=
.
通过三关或通过甲、丙两关但乙关没通过,
∴获奖的概率P=
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 9 |
| 1 |
| 9 |
| 1 |
| 3 |
(2)由已知得ξ=0,1,2,3,
P(ξ=0)=(1-
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 18 |
P(ξ=1)=
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 5 |
| 18 |
P(ξ=2)=
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 4 |
| 9 |
P(ξ=3)=
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 9 |
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 18 |
| 5 |
| 18 |
| 4 |
| 9 |
| 2 |
| 9 |
| 15 |
| 6 |
点评:本题考查获奖的概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,是中档题.

练习册系列答案
相关题目
已知函数f(x)的导函数的图象如图所示,则下列判断中正确的是( )
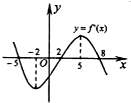

| A、函数f(x)在区间(-2,2)内单调递增 |
| B、函数f(x)在区间(-5,2)内单调递减 |
| C、函数f(x)在区间(5,8)内单调递减 |
| D、函数f(x)在区间(-2,5)内为单调函数 |
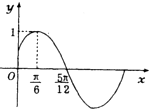 已知函数f(x)=Asin(ωx+φ)(a>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(a>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=sin(3x+
| ||
B、f(x)=sin(2x+
| ||
C、f(x)=sin(x+
| ||
D、f(x)=sin(2x+
|