Question

10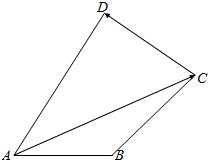．如图，四边形ABCD中，AB=1，AD=2，BC=DC，∠DAB=$\frac{π}{3}$，∠DCB=$\frac{π}{2}$，则$\overrightarrow{AC}$•$\overrightarrow{CD}$=-$\frac{\sqrt{3}}{2}$．

Answer 1

分析 连结BD，则可证AB⊥BD，建立平面直角坐标系求出$\overrightarrow{AC}，\overrightarrow{CD}$的坐标，代入数量积公式计算即可．

解答 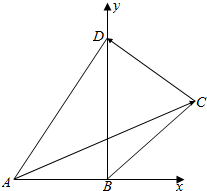解：连结BD，在△ABD中，由余弦定理得BD=$\sqrt{{1}^{2}+{2}^{2}-4cos\frac{π}{3}}$=$\sqrt{3}$，∴AB⊥BD．
∵BC=DC，∠DCB=$\frac{π}{2}$，∴BC=$\frac{\sqrt{6}}{2}$，∠ABC=$\frac{π}{2}+\frac{π}{4}$=$\frac{3π}{4}$．
以AB，BD为坐标轴建立平面直角坐标系，如图，则A（-1，0），C（$\frac{\sqrt{3}}{2}$，$\frac{\sqrt{3}}{2}$），D（0，$\sqrt{3}$）．
∴$\overrightarrow{AC}$=（$\frac{\sqrt{3}}{2}+1$，$\frac{\sqrt{3}}{2}$），$\overrightarrow{CD}$=（-$\frac{\sqrt{3}}{2}$，$\frac{\sqrt{3}}{2}$）．
∴$\overrightarrow{AC}$•$\overrightarrow{CD}$=（$\frac{\sqrt{3}}{2}+1$）×（-$\frac{\sqrt{3}}{2}$）+$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{3}}{2}$=-$\frac{\sqrt{3}}{2}$．
故答案为-$\frac{\sqrt{3}}{2}$．

点评 本题考查了平面向量的数量积运算，建立坐标系可以简化计算．