题目内容
1.函数y=$\frac{3}{2}$x-1,如果y<0,则x的取值范围是(-∞,$\frac{2}{3}$).分析 根据解析式得出不等式$\frac{3}{2}$x-1<0,求解得出x$<\frac{2}{3}$,即可得出答案.
解答 解:∵函数y=$\frac{3}{2}$x-1,y<0,
∴$\frac{3}{2}$x-1<0,x$<\frac{2}{3}$,
∴x的取值范围(-∞,$\frac{2}{3}$),
故答案为;(-∞,$\frac{2}{3}$).
点评 本题简单的考查了函数不等式的关系,属于简单题目,准确求解书写即可.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
11.设x0为函数f(x)=sinπx的零点,且满足|x0|+|f(x0+$\frac{1}{2}$)|<33,则这样的零点有( )
| A. | 61个 | B. | 63个 | C. | 65个 | D. | 67个 |
16.如果关于x的不等式ax2-丨x+1丨+2a<0的解集为空集,则实数的取值范围是( )
| A. | [$\frac{1+\sqrt{3}}{4}$,+∞) | B. | [2,+∞) | C. | [$\frac{\sqrt{3}-1}{4}$,+∞) | D. | (-∞,2] |
9.已知变量x,y满足约束条件$\left\{\begin{array}{l}x+2y≥2\\ 2x+y≤4\\ y≤2\end{array}\right.$则目标函数z=3x-y的最大值( )
| A. | 6 | B. | $\frac{3}{2}$ | C. | -1 | D. | $-\frac{3}{2}$ |
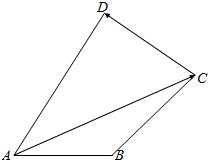 如图,四边形ABCD中,AB=1,AD=2,BC=DC,∠DAB=$\frac{π}{3}$,∠DCB=$\frac{π}{2}$,则$\overrightarrow{AC}$•$\overrightarrow{CD}$=-$\frac{\sqrt{3}}{2}$.
如图,四边形ABCD中,AB=1,AD=2,BC=DC,∠DAB=$\frac{π}{3}$,∠DCB=$\frac{π}{2}$,则$\overrightarrow{AC}$•$\overrightarrow{CD}$=-$\frac{\sqrt{3}}{2}$.