题目内容
15.已知a>0,b>0,$\frac{1}{a}$+$\frac{1}{b}$≤4,(a-b)2=16(ab)3,那么a+b=2.分析 令s=a+b,t=ab,则$\frac{1}{a}$+$\frac{1}{b}$≤4,得s≤4t.由(a-b)2=16(ab)3,得,(a+b)2-4ab=16(ab)3,s2≥s+$\frac{1}{4}$s3,化简解出即可得出.
解答 解:令s=a+b,t=ab,
则$\frac{1}{a}$+$\frac{1}{b}$≤4,得s≤4t,
由(a-b)2=16(ab)3,得,(a+b)2-4ab=16(ab)3,
∴s2-4t=16t3
即s2=4t+16t3≥s+$\frac{1}{4}$s3,
∴s2-4s+4≤0,
解之得s=2.
即a+b的值等于2.
故答案为:2.
点评 本题考查了基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
5.在△ABC中,角A、B、C的对边分别是a、b、c,$\frac{asinA+bsinB-csinC}{sinBsinC}$=$\frac{2\sqrt{3}}{3}$a,a=2$\sqrt{3}$,若b∈[1,3],则c的最小值为( )
| A. | 2 | B. | 3 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
2.某产品的广告费用x与销售额y的统计数据如表:
根据表格已得回归方程为$\widehat{y}$=9.4x+9.1,表中有一数据模糊不清,请推算该数据的值为37.
| 广告费x(万元) | 2 | 3 | 4 | 5 |
| 利润y(万元) | 26 |  | 49 | 56 |
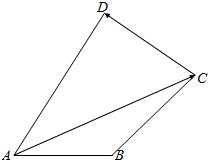 如图,四边形ABCD中,AB=1,AD=2,BC=DC,∠DAB=$\frac{π}{3}$,∠DCB=$\frac{π}{2}$,则$\overrightarrow{AC}$•$\overrightarrow{CD}$=-$\frac{\sqrt{3}}{2}$.
如图,四边形ABCD中,AB=1,AD=2,BC=DC,∠DAB=$\frac{π}{3}$,∠DCB=$\frac{π}{2}$,则$\overrightarrow{AC}$•$\overrightarrow{CD}$=-$\frac{\sqrt{3}}{2}$.