题目内容
5.已知正方形的中心G(2,1),正方形有一边所在直线方程是l:x-y+1=0,求其它三边所在直线的方程.分析 根据直线的位置关系设出直线方程,根据G到四边的距离相等列方程解出.
解答 解:设与l平行的边所在直线方程为x-y+a=0(a≠1),与l垂直的两边所在直线方程分别为x+y+b=0,x+y+c=0,
则G到四条直线的距离相等,∴$\frac{2}{\sqrt{2}}$=$\frac{|1+a|}{\sqrt{2}}$=$\frac{|3+b|}{\sqrt{2}}$=$\frac{|3+c|}{\sqrt{2}}$,解得a=-3,b=-1,c=-5.
∴其余三边所在直线方程分别为x-y-3=0,x+y-1=0,x+y-5=0.
点评 本题考查了直线的位置关系与斜率的关系,点到直线的距离公式,属于基础题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
16.如果关于x的不等式ax2-丨x+1丨+2a<0的解集为空集,则实数的取值范围是( )
| A. | [$\frac{1+\sqrt{3}}{4}$,+∞) | B. | [2,+∞) | C. | [$\frac{\sqrt{3}-1}{4}$,+∞) | D. | (-∞,2] |
20.已知直线a⊥直线b,b⊥直线c,c⊥a,直线l与a,b所成的角分别为45°,60°,则l与c所成的角为( )
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
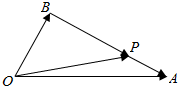 如图,在△OAB中,已知P为线段AB上一点,$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$.
如图,在△OAB中,已知P为线段AB上一点,$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$.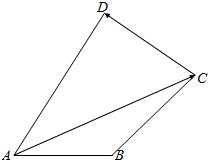 如图,四边形ABCD中,AB=1,AD=2,BC=DC,∠DAB=$\frac{π}{3}$,∠DCB=$\frac{π}{2}$,则$\overrightarrow{AC}$•$\overrightarrow{CD}$=-$\frac{\sqrt{3}}{2}$.
如图,四边形ABCD中,AB=1,AD=2,BC=DC,∠DAB=$\frac{π}{3}$,∠DCB=$\frac{π}{2}$,则$\overrightarrow{AC}$•$\overrightarrow{CD}$=-$\frac{\sqrt{3}}{2}$.